Generative Models

https://deepgenerativemodels.github.io/ 스탠포드 대학의 수업이라고하는데 참고해서 수업을 진행하셨다.

Generative model

단순히 이미지와 문자를 만드는 것이 아니다.

강아지 이미지들을 받았다고 해보자.

Generative model에 probability distribution \(p(x)\)를 학습할 것을 기대할 수 있다.

• Generation: \(x_{new} \sim p(x)\)를 샘플링 했을 때, \(x_{new}\)는 개처럼 보여야한다.
• Density estimation: \(p(x)\)를 사용해서 임의의 입력 \(x\)에 대해서 개인지, 혹은 개가 아닌지, 고양이인지 등의 판단이 가능하다. (anomaly detection, 이상행동 감지)
  • 엄밀한 의미에서 Generative model은 Descriminator model을 포함하고 있다.
  • 확률값을 얻을 수 있는 모델을 _explicit model_이라고 한다.
• Unsupervised representation learning(feature learning): feature를 unsupervised 방식으로 학습하는 것
  • 교수님은 의아하다고 하지만 스탠포드 대학 강의에서는 이 또한 generative model이 지향하는 것이라고 했다고 한다.

Basic Discrete Distributions

시작하기 전에 알아둬야할 간단한 수학적 지식이다. 앞서 임성빈 교수님 수업에서도 말씀해주셨던 내용이지만 복습하는 의미로 적는다.

Bernoulli distribution

Bernoulli에는 1개의 paramter만 필요하다.

• D = {Heads, Tail}
• P(X=Heads) = p, then P(X=Tails) = 1 - 0
• Write: X ~ Ber(p)

Categorical distribution

Categorical에는 m-1개의 parameter가 필요하다. m-1개의 요소들을 안다면, 나머지 1개의 요소는 자동적으로 결정되기 때문이다.

• D = {1, …, m}
• P(Y=i) = \(p_i\), such that $\sum_{i=1}^m p_i$ = 1
• Write: Y ~ Cat(p1, …, pm)

RGB

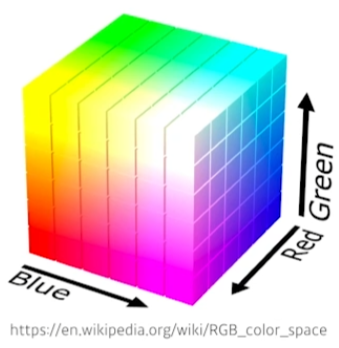
• $(r, g, b) \sim p(R, G, B)$
• number of cases = 256 x 256 x 256
• number of parameters = 256 x 256 x 256 - 1
  • 1개의 rgb 픽셀을 표현하기 위한 parameter의 수는 매우 많다! 당연한 이야기지만..

Binary image

• n pixel의 binary image를 가정해보자.
• $2^n$ state가 필요하다.
• Sampling from $p(x_1, …, x_n)$ generate an image.
  • $p(x_1, …, x_n)$를 샘플링하기 위해서는 $2^n - 1$의 parameters가 필요하다.

---

즉, parameter의 수가 너무 많다. 줄여볼 수 없을까?

Structure through independence

Binary image에서 $X_1, …, X_n$이 independent하다고 가정해보자. 사실 말이 안된다. 모든 픽셀이 independent하다면 표현할 수 있는 이미지는 화이트 노이즈일 뿐일 것이다. 하지만 그래도 가정해보자.

$p(x_1, …, x_n) = p(x_1)p(x_2)…p(x_n)$

이 때, possible state의 수는 동일하게 $2^n$이다.

하지만 $p(x_1, …, x_n)$를 위한 parameter의 수는 n개이다. 왜냐하면 각각의 픽셀에 대해서 필요한 parameter의 수는 1개이다. 또한 모두 independent하기 때문에, 모두 더하면 n이다.

Chain rule

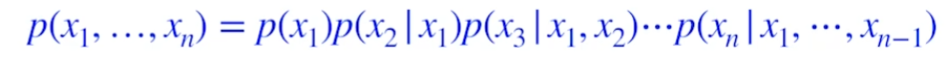
그 어떤 가정도 필요없는 정리이다. 즉, 기본적인 출발선에서 시작하기 때문에 fully dependent model이라고 생각하자.

모든 parameter의 수는 $2^n -1 $이다. exponential reduction을 했다!

Bayes’ rule

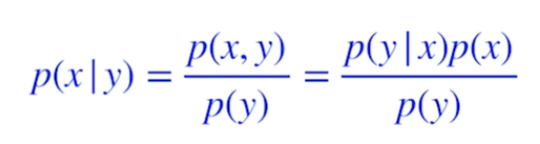
Conditional independence

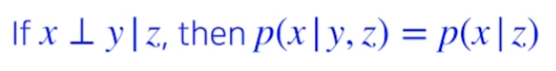x and y are conditional independent given z, p of x given y and z는 p of x given z와 같다. 라고 영어로 말하시더라.

z가 주어지고 x와 y가 indepedent하다면, random한 x를 볼 때 y는 상관없다는 것이다.

즉, chain rule이나 혹은 다른 수식에서 independent한 관계인 변수들이 있다면 조건부에서 날려주는 역할을 하는 정리이다. 이 정리를 사용해서 fully depedent model과 fully independent model 사이의 좋은 모델을 만들 것이다.

Markov assumption

chain rule에 Markov assumption을 적용해보자. RNN에 나왔던 가정인거 같은데, 현재 상태를 바로 이전의 상태만을 활용해서 정의하는 것이다. 즉, chain rule에서 이전의 모든 정보를 활용하는 항들이, n시점에서는 n-1만을 참조하는 항들로 바뀐다.

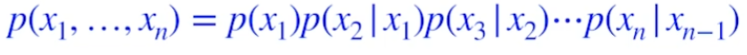
모든 parameter의 수는 $2n-1$이다.

fully independent하게 계산했던 parameter의 수인 n과 비교하면 크지만, dependent하게 계산했던 chain rule인 $2^n-1$에 비하면 exponential reduction하다.

즉, 이러한 형태로 중간의 sweet spot을 찾는 것이 auto-regressive model.

Auto-regressive model

• 28x28의 binary image를 사용한다고 가정.
• $p(x) = p(x_1, …, x_785)$를 $x\in{0,1}^{784}$에서 학습하는 것.
• $p(x)$를 어떻게 parametrize할 것인가?
  • chain rule을 사용해 joint distribution을 나눈다.
  • 
  • 이것을 _autoregressive model_이라고 한다.
  • markov assumption처럼 바로 이전의 정보만을 활용하는 것도 autoregressive model이다.
• 모든 random variables에 대해 순서를 부여해야한다.
  • 순서에 따라 성능이 달라지기도 한다.

이전 1개만 고려하는 모델 = AR(1) model 이전 n개를 고려하는 모델 = AR(N) model

NADE

Neural autoregressive density estimator

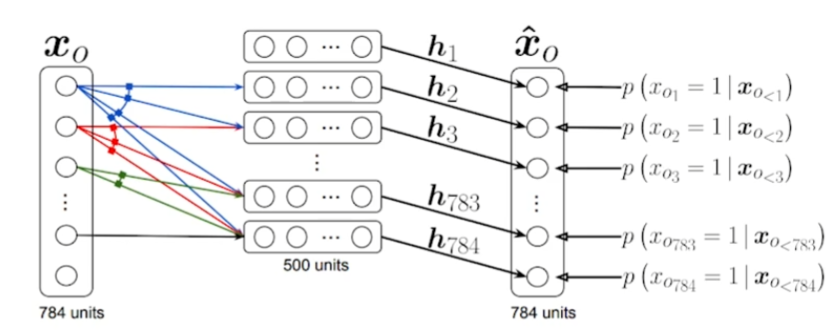
i번째 픽셀을 첫번째 ~ i-1번째 픽셀에 dependent하게 구성.

• 첫번째 픽셀에 대한 확률분포를 어느 것에도 dependent하지 않게 구성.
• 두번째 픽셀에 대한 확률분포는 첫번째 픽셀에만 dependent하게 구성.
• 다섯번째 픽셀에 대한 확률분포는 첫번째 ~ 네번째 픽셀에만 dependent하게 구성.
• i번째 픽셀은 i-1개의 픽셀에 dependent하다.
• 입력차원이 달라지면서 weight는 게속 커진다.
  • i번째 입력은 i-1개의 입력을 받을 수 있는 weight가 필요하니까.
• 마지막 layer에 ‘a mixture of Gaussian’을 써서 continuous random variables를 만들 수도 있다.

NADE는 explicit model이다. chain rule처럼 확률이 계산되기 때문에, 어떻게든 확률을 계산할 수 있다.

inplicit model은 generation만 할 수 있다.

Pixel RNN

RNN을 auto-regressive하게 만들자.

n x n RGB image에 대한 수식은 다음과 같다.

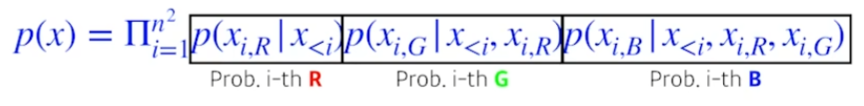
Ordering에 따라서 두가지로 나뉜다.

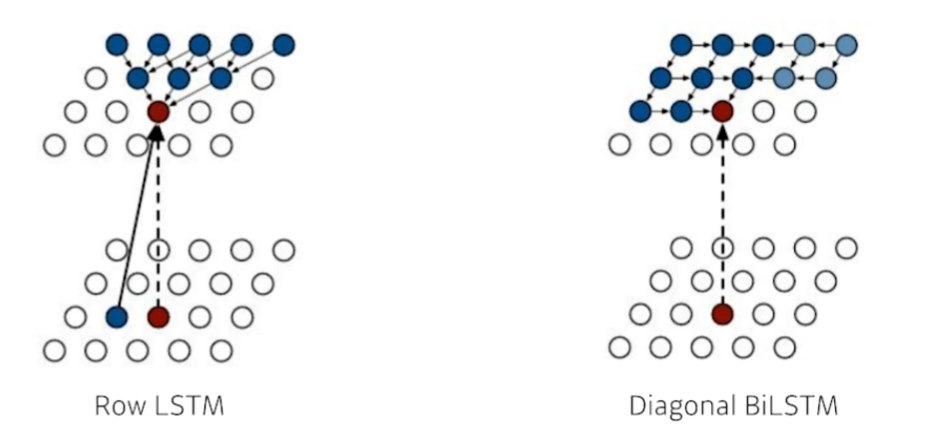
• Row LSTM
  • 위 쪽의 정보들을 활용
• Diagonal BiLSTM
  • 이전의 모든 정보들을 활용