[HackerRank] Sherlock and Cost

https://www.hackerrank.com/challenges/sherlock-and-cost/problem

풀이

ref: Blog

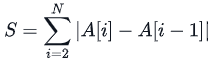
위 수식을 최대화하는 \(A\)를 구하면 된다. diff의 차이를 극대화하는 것이기 때문에 A[i]는 B[i]나 1이 되면 된다. 왜냐하면 $1 <= A[i] <= B[i]$이기 때문이다.

bfs, dfs를 통해 A[i]의 모든 가능성을 brute-force하게 검색할 수도 있지만 $n = 10^5$이기 때문에 time limit에 걸린다. Dynamic programming을 통해 S[i]를 계속 갱신하면서 최대 S[i]를 찾는다.

cost함수에서는 가장 큰 S의 요소를 반환하면 된다.

S 갱신

A[i]가 선택할 수 있는 값의 경우는 다음과 같다.

• 1
• B[i]

이러한 경우의 수는 A[i - 1] 또한 마찬가지이다.

S[i]를 일반화하면 다음과 같다. $S[i] = S[i - 1] + A[i]$

이 때, A[i]의 경우의 수가 2가지이므로 A[i - 1]의 경우의 수도 2가지이다. 따라서 A[i]가 고정된 경우, S[i]에 대한 경우의 수는 2가지이다. S[i]에서 선택할 수 있는 경우의 수는 다음과 같다.

• $A[i] = 1$, $S[i][0]$
  • $A[i - 1] = 1, S[i - 1][0] + (1 - 1)$
  • $A[i - 1] = B[i - 1], S[i - 1][1] + abs(B[i - 1] - 1)$
• $A[i] = B[i]$, $S[i][1]$
  • $A[i - 1] = 1, S[i - 1][0] + abs(B[i] - 1)$
  • $A[i - 1] = B[i - 1], S[i - 1][1] + abs(B[i] - B[i - 1])$

위와 같은 점화식을 구성하면 S[i]에는 순차적으로 이전 정보들의 누적되면서 새로운 S[i]가 갱신된다.

코드

https://github.com/naem1023/codingTest/blob/master/dp/hackerrank-sherlock-and-cost.py