AutoML
Data Engineering
- Data Cleansing, Preprocessing
- Feature Engineering
- Select ML Algorithm
- DL: Select Backbone Model
- Set Hyperparameters
- DL: Loss, Optimzier, Learning rate, batch size
model architecture와 hyperparameter 선정은 train/evaluate에 대한 피드백을 받고 재선정하게 된다. 이러한 과정을 사람이 직접 수행하는게 일반적이다. 이러한 일련의 과정에서 사람을 제거하고 자동화하는 것이 AutoML의 목표이다.
Definition

AutoML의 목표를 설명하면서 서술했던 말을 수식으로 명시화한 것이다. hyperparameter, ML algorithm, data들이 주어져있을 때 loss를 minimize하는 hyperparmeter configuration을 찾는 것이 HPO(Hyperparameter Optimization = AutoML)의 목표이다.
경량화의 다른 관점
- 기존 모델을 경량화
- Pruning, Tensor decomposition
- Searching을 통해 경량 모델을 찾는 기법
- NAS(Neural Architecture Search), AutoML
AutoML은 경량모델을 찾는 기법이다!
DL Model Configuration
Type
- Categorical
- Optimizer: Adam, SGD, AdamW …
- Module: Conv, BottleNeck, InvertedResidual
- Continuous
- learning rate, regularizer param, …
- Integert
- Batch size, epochs
Conditional configuration
configuration에 따라서 search spaec가 달라진다.
- Batch size, epochs
- Optimizer에 따라서 optimizer parameter의 종류와 search space가 달라진다.
- Module sample(Vanilla conv, BottleNeck, InvertedResidual)에 따라서 모듈별 parameters와 search space가 달라진다.
AutoML Pipeline
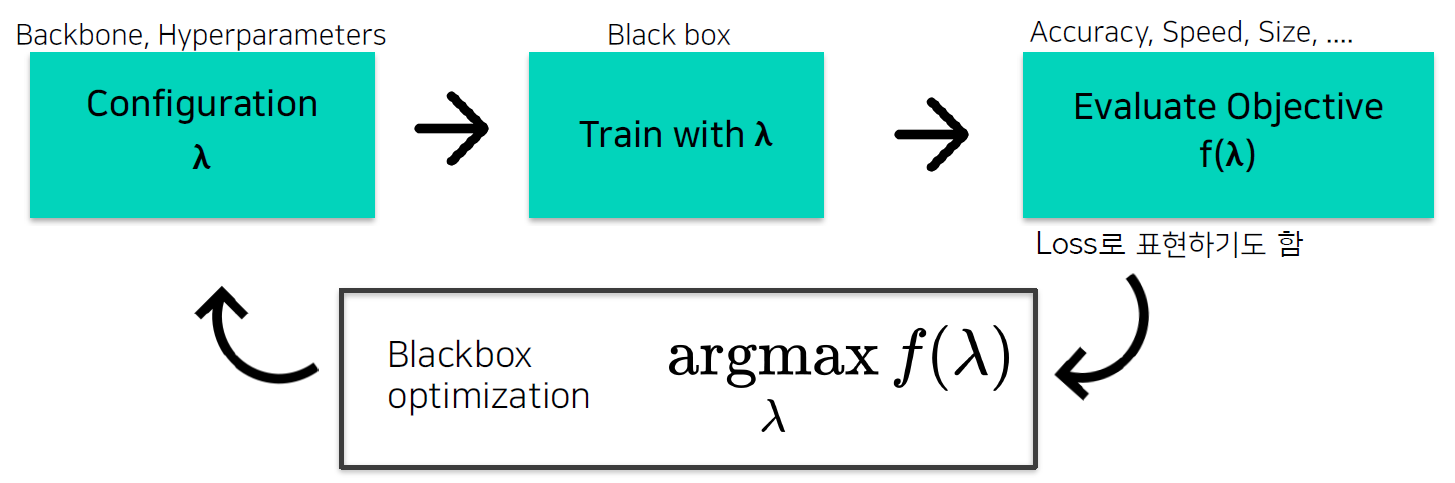
앞서 서술했던 HPO의 정의와 유사하다. 추가된 점은 Evaluate Objective function인 $f$이다. $f$의 정의는 다양할 수 있다. 모델의 사이즈만이 작아지는 것을 원할 수도 있고, 모델의 성능만이 향상되는 것을 원할 수도 있고 여러 목표치가 혼합된 형태일 수도 있다.
이러한 목표들을 maximize하도록 Blackbox optimization을 진행해서 새로운 configuration $\lambda$를 찾는다.
Bayesian Optimization(BO)
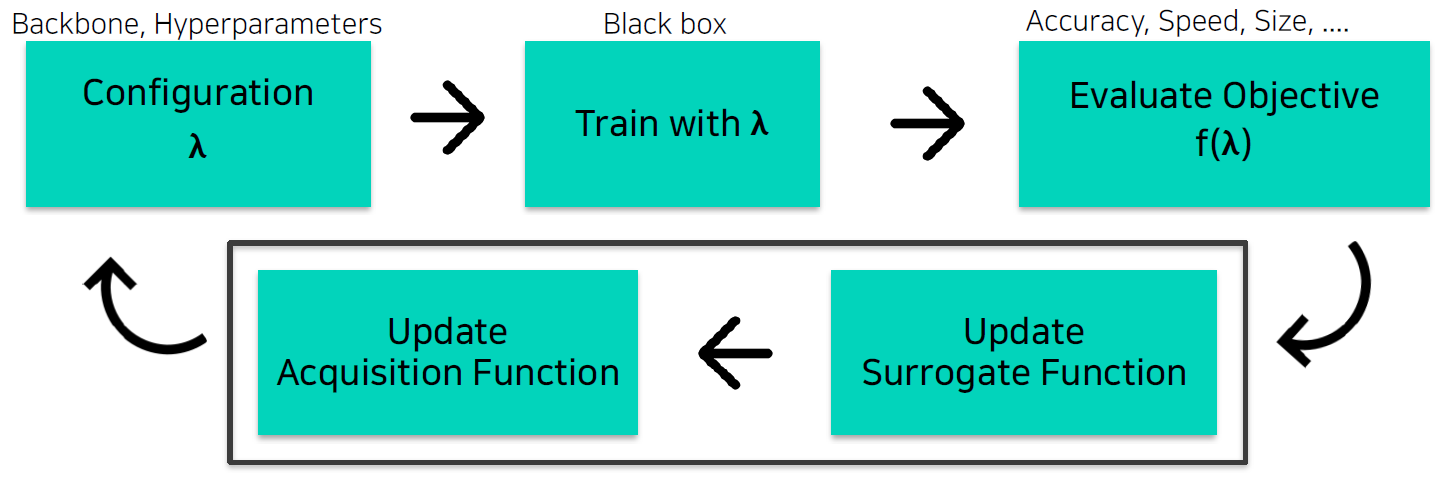 Blackbox 형태의 optimization을 위와 같이 구성한 것이다.
Blackbox 형태의 optimization을 위와 같이 구성한 것이다.
- Surrogate function: $f(\lambda)$를 예측하는 regression model. 정확히 예측이 가능해진다면 다음에 시도할 $\lambda$ 더 잘 결정할 수 있을 것이다.
- Acquisition function: 다음에 시도할 $\lambda$를 결정해준다.
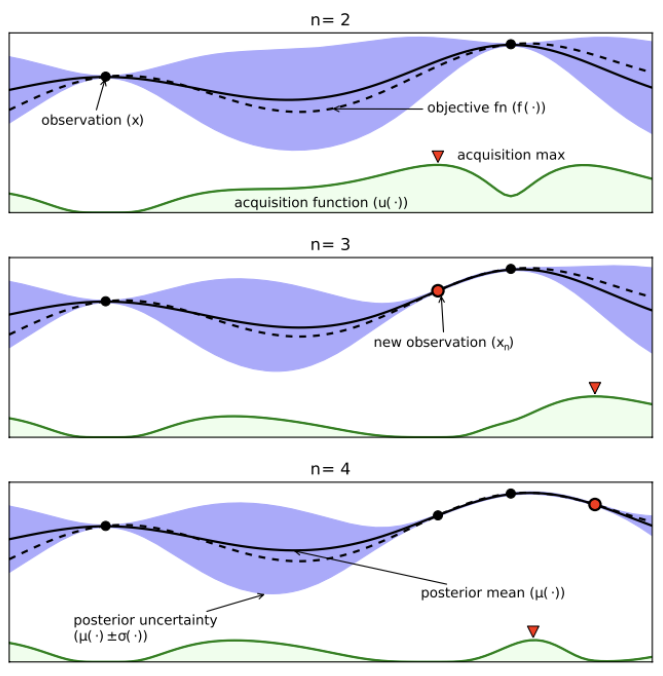
도식도의 과정을 순서대로 나열하면 아래와 같다.
- $\lambda$(x)를 sample(observation)
- 해당 configuration으로 DL 모델 학습
- objective 계산. 위 그림에서의 observation(x)가 이것에 해당한다.
- Surrogate model update. 위 그림에서 실선과 보라색 영역으로 표현되는 것들이다. e.g., GP(Gaussian Process) model, posterior mean, jposterior varicance(uncertainty)
- Acquisition function update. 위 그림에서 초록색으로 표현되는 영역이다. surrogate model의 추세를 보고 가장 좋은 다음 $\lambda$를 예측한다.
BO with GPR
Gaussian Process Regression
불확실성(uncertainty)을 모델링할 수 있는 방법이다. BO에서 사용한 그래프에서 Surrogate model의 두 지점만을 알고 있고 이외의 지점에 대해서는 불확실하다. 이 때, GP를 사용해서 값을 알고 있는 두 지점 외의 값들에 대해서, 범위를 얻을 수 있다.
일반적인 Regression taks Set of train data: $(X,Y)$ Set of test data: $(X_,Y_)$ $Y\approx f(X) + e$
GP의 아이디어
- 알고자 하는 특정 위치의 $Y_$ 값은 이미 알고 있는 $X,Y,X_$와 연관이 있지 않을까?
- positive, negative 관계 무관
- $X,Y,X_$값으로부터 $Y_$를 추정하는 표현을 Kernel 함수 $K$로 표현해보자!
GP의 엄밀하지 않은 정의
- $f(x)$: input x에 대한 Random variable로 정의 = input x에 대해서 가능한 함수들의 분포
- Random variable의 distribution: Multivariate Gaussian distribution
정의만 서술하면 위와 같이 되고, $f(x)$에 대한 정의를 GP에서 어떻게 생각했는지 풀어쓰면 아래와 같다.
- 함수들의 분포를 정의. 이 분포가 Multivariate Gaussian distribution을 따른다고 가정.
- = 함수 $f$가 Gaussian process를 따른다.
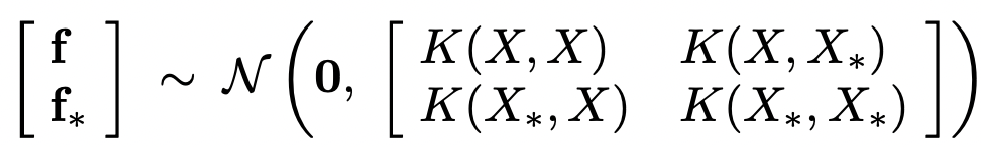
지금 설명된 내용을 수식으로 정리하면 위 수식이 된다.
해당 수식에서는 Gaussian Identities가 적용된다고 한다. Gaussian의 margianl과 conditional도 Gaussian을 따른다는 정의다.
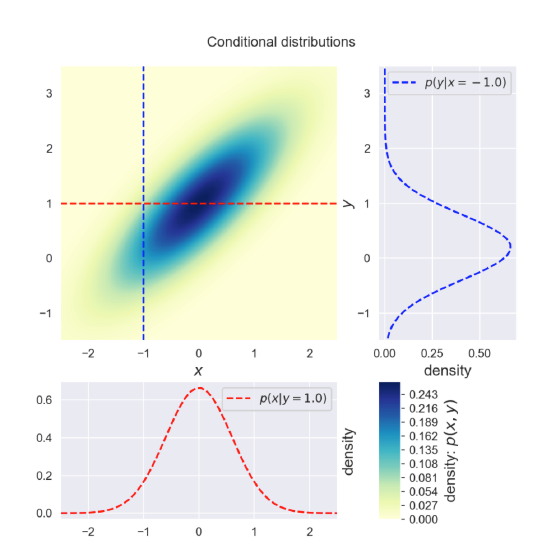
이를 그림으로 위 처럼 그림으로 생각할 수 있다. conditional의 어떤 쪽에서 본래 Gaussian을 바라본다고 해도, 해당 conditional 또한 Gaussian을 따른다.
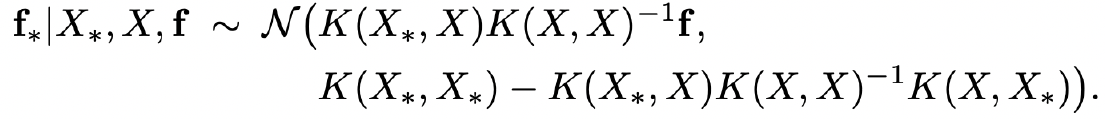
수식으로 설명한 GP를 통해 알 수 있는 사실은 $X_, X, f$가 주어졌을 때 $f_$의 평균과 분포를 알 수 있다는 것이다.
Surrogate Model
앞서 정리한 내용들을 활용해 Surrogate model에 대한 보다 자세한 정리를 해보자.
- def: Objective $f(\lambda)$를 예측하는 모델
- 관측된 $f(\lambda)$를 활용해, 새로운 $\lambda_$에 대한 objective $f(\lambda_)$f를 예측
- Surrogate model을 학습해서, 다음 step의 좋은 $\lambda$를 선택하는 기준으로 사용
- 대표적 Surrogate model
- GPR(Gaussian Process Regression) model
- mean: 예측 $f$값, var: uncertainty
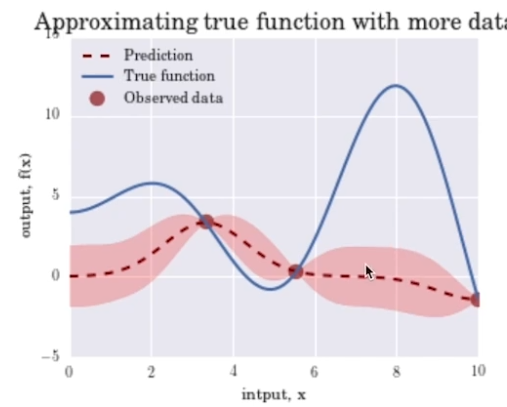
- mean: 예측 $f$값, var: uncertainty
- GPR(Gaussian Process Regression) model
Observation data가 늘어날수록 uncertainty가 줄어들면서 true function에 prediction이 fitting된다.
Acquisition Function
- def: Surrogate model의 ouput을 활용해 다음에 시도하면 좋은 $\lambda$를 결정하는 함수
- Exploration, Exploitation 사이의 적절히 balancing 할 수 있도록 수식이 구성됐다. 둘 사이의 분배는 heuristic하게 결정한다.
- Exploration: 불확실한 지점을 탐색
- Exploitation: 알고 있는 가장 좋은 곳을 탐색
- 갱신된 Acquistion function의 max 지점을 다음 iteration에서 시도
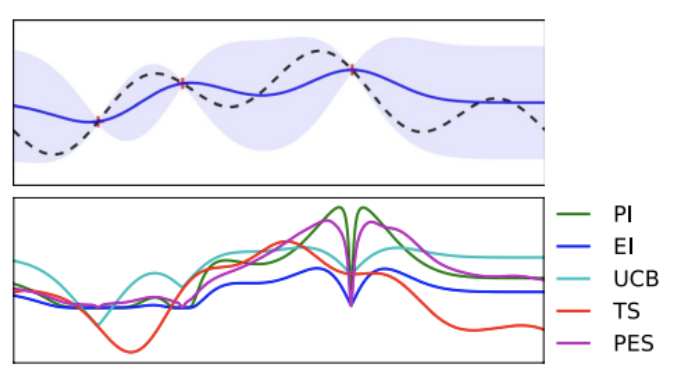
위쪽 그래프는 surrogate model이고 아래 그래프가 acquisition function 그래프이다. acquisition function의 값들이 특정 지점에서 굉장히 작아지고 해당 값 부근에서는 값이 커진다. Exploitation 관점에서 이미 알고 있는 지점은 탐색할 필요가 없고 이미 알고 있는 값 부근이 가장 좋은 탐색 포인트이기 때문이다. 이러한 방식으로 Acquisition function이 구성된다.
e.g., Upper Confidence Bound(UCB)
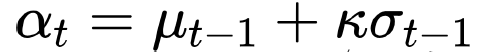
- $\mu$: posterior mena(=Exploitation)
- $\sigma$: posterior variance(=Exploration)
- $\kappa$: balancing parameter
BO with TPE
GP의 문제점
- Complexity: $O(N^3)$
- Conditional, continuous/discrete parameter들이 혼합될 때 적용이 어려움 대부분 두번째에서 어려움이 많이 발생하고 요즘은 TPE를 많이 사용한다고 한다.
TPE(Tree-structured Parzen Estimator)와 GPR의 차이
-
GPR: $p(f \lambda)$(posterior distribution)을 계산 -
TPE: $p(\lambda f)$(likelihood), $p(\lambda)$(prior)를 계산

Leave a comment