Gradient descent 기본

여러번 notion에 정리했던 내용인데 부캠에서 배운 내용 중심으로 다시 정리해봤다.

미분

import sympy as sym
from sympy.abc import x

sym.diff(sym.poly(x**2 + 2*x + 3), x)

Gradient ascent(경사상승법)

f(x) 미분값을 x에 더하며 함수의 극대값의 위치를 구할 때 사용. 즉, 목적함수를 최대화해야 할 때 사용.

Gradient descent(경사하강법)

f(x) 미분값을 x에 빼면서 함수의 극소값의 위치를 구할 때 사용. 즉, 목적ㅎ마수를 최소화해야 할 때 사용.

Algorithm

# gradient: 미분을 계산하는 함수
# init: 시작점
# lr: 학습률
# eps: 입실론

var = init
grad = graident(var)
while (abs(grad) > eps):
	var = var - lr * grad
    grad = gradient(var)

미분값이 0이 되는 것이 목표지만, 컴퓨터로 이를 표현할 수 없다. 따라서 매우 작은 실수값인 입실론을 종료 조건으로 설정한다.

Partial differentiation(편미분)

ML에서 다루는 변수는 보통 벡터이기에, 일반적인 미분이 아니라 편미분을 통해 방향성을 확보한다. 고등학교 때 했던대로 하면 된다.

undefined

이 때 ei는 i번째 값만 1이고 나머지는 0인 단위 벡터이다. 즉, 원하는 곳의 정보만 필터링해서 미분하게 해준다.

gradient vector

nabla

벡터를 변수로 사용하는 함수라면 편미분을 사용해서 미분을 해야하는데, 이 때 변수들이 매우 많아진다.

따라서, 모든 변수에 대한 편미분을 시행한 결과를 다시 벡터로 모아서 이를 gradient descent에 사용한다. 이를 gradient 벡터라고 하는데 한꺼번에 모든 변수에 대한 업데이트가 가능하다는 장점이 있다.

undefined

해당 기호를 nabla라고 한다.

gradient vecotr 시각화

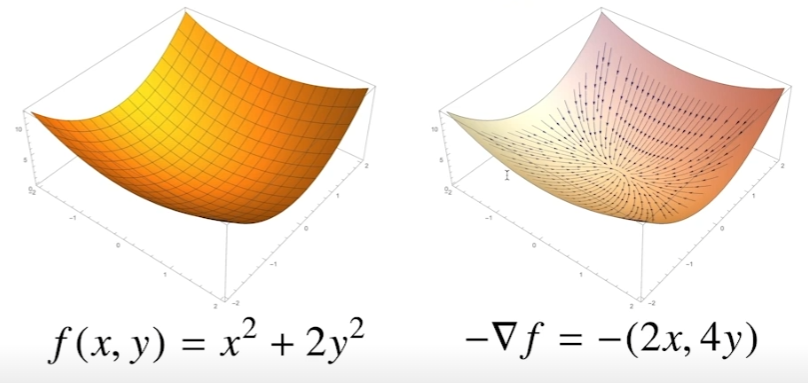
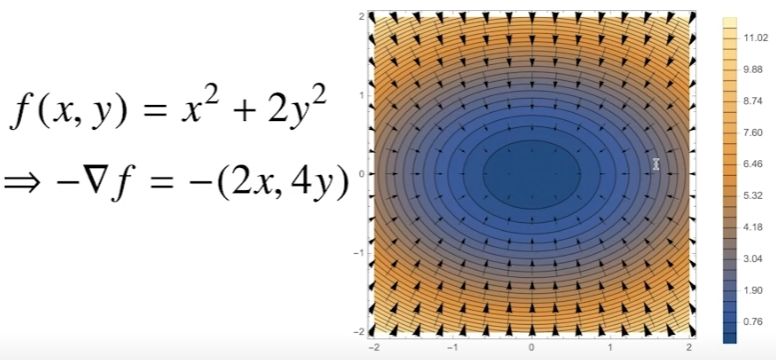
등고선으로 표시하면 이해가 쉽다. 등고선을 기준으로 벡터의 방향은 원점으로 가장 빨리 감소하는 방향으로 표시된다.

Algorithm using gradient vector

# gradient: gradient vector를 계산하는 함수
# init: 시작점
# lr: 학습률
# eps: 입실론

var = init
grad = graident(var)
while (norm(grad) > eps):
	var = var - lr * grad
    grad = gradient(var)

달라진 점은 gradient의 정의와 종료조건 계산시 abs 대신 norm을 사용하는 것이다.