Sungho Park

AI

부캠 강사님께서 용어에 대해 확실히 알고 가라고 하셨다.

어제(21.08.09) 선택과제 2번의 AAE에 대해서 알아보다가 기겁을 했다. 한 문장 안에서 모르는 단어를 세는 것보다, 아는 단어를 세는게 빨랐다. 분명 영어로 쓰여있는데 외계어 같았다…

인턴을 하면서, 졸업프로젝트를 하면서 혼자 독학으로 잡다하게 지식을 쌓아올린 폐해라고 생각한다. ML 분야에서 사용되는 용어들만이라도 확실하게 알고 있자.

그런 의미로 알고 있던 용어들이라도 수업에서 다뤘던 것들은 모두 기술했다.

Introduction

Gradient descent

undefined

First-order iterative optimization algorithm for finding a local minimum of a differentiable function.

Hyper parameter

parameter : 가중치, bias, convolution weight 등 학습이 되면서 업데이트 되는 것들. hyper parameter : learning rate, network의 크기, loss function의 종류 등 개발자가 직접 정하는 것들.

Generalization

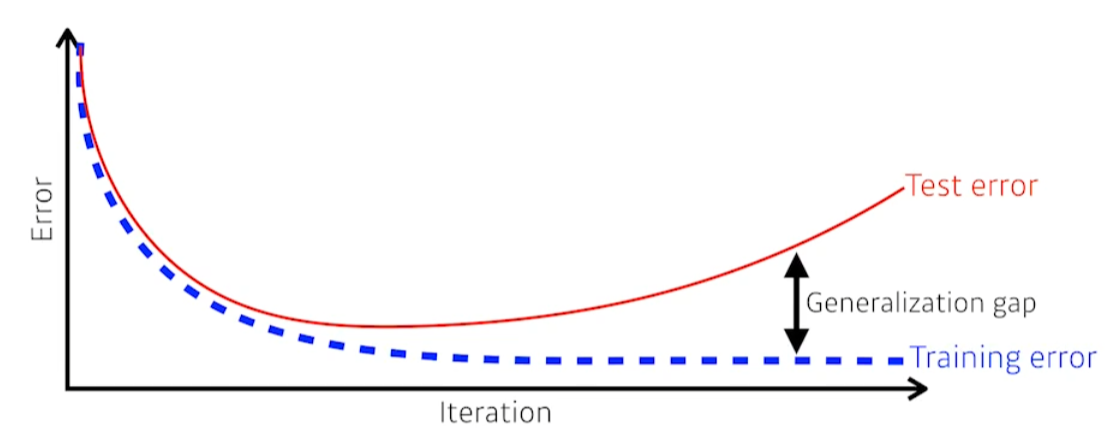보통 학습이 오래 지속되면 test error는 증가한다. train과 test 사이의 성능 gap을 Generalizaiton gap이라고 한다.

Generalization performance가 좋다. = 모델의 성능이 학습 데이터를 사용했을 때와 비슷함을 보장.

하지만, Generalization performance가 좋다고 모델의 성능이 좋음을 보장하지는 않는다. 왜냐하면 학습 데이터가 제대로 학습되지 않은 모델임에도 Generalization performance는 좋을 수 있기 때문이다.

Underfitting, Overfitting

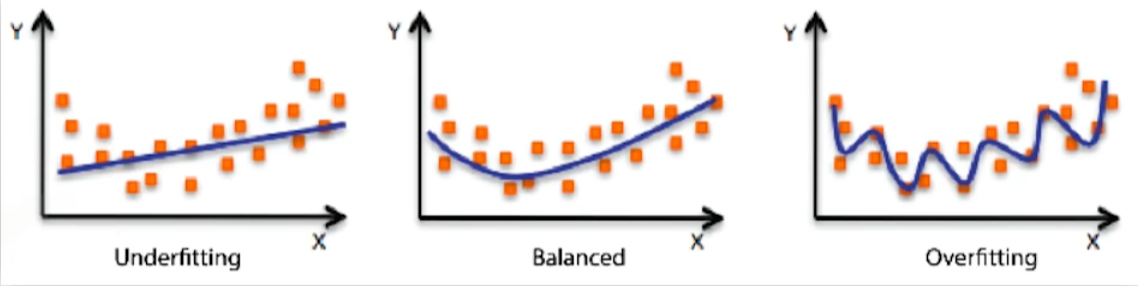Overfitting(과적합) : 학습 데이터에서는 모델이 잘 작동하지만, 실제 성능은 좋지 않은 것. Underfitting : 학습이 제대로 되지 않아, 학습조차 제대로 안된 것.

물론, 위 그림은 concept만을 명시한 것이다. 즉, Overfitting의 예시 도표가 실제로는 우리가 원하는 결과일 때도 분명 존재한다는 것이다. 문제의 정의, 도메인 지식 등 여러가지를 살려서 판단하자.

Cross-validation

K-fold validation. 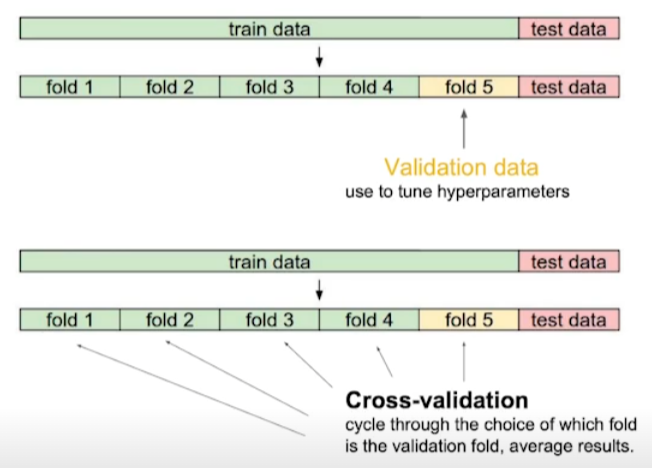ref: https://blog.quantinsti.com/cross-validation-machine-learning-trading-models/

  1. train data를 k개로 구분한다.
  2. k-1개를 train에 사용한다.

  3. 나머지 1개를 validation에 사용한다.

hyper parameter에 대한 clue는 보통 없다! 그래서 cross validation을 통해 최적의 hyper parameter 조합을 찾는다.

최적의 hyper parameter를 찾으면, hyper parameter를 고정 후 모든 학습 데이터를 활용해 학습한다.

당연하지만 test data는 어떠한 방식으로든 학습에서 활용하면 안된다. 엄연히 cheating과도 같은 행위이다. 물론 cheating을 한다고 좋은 모델을 만든다고 보장할 수도 없다.

Bias, Variance

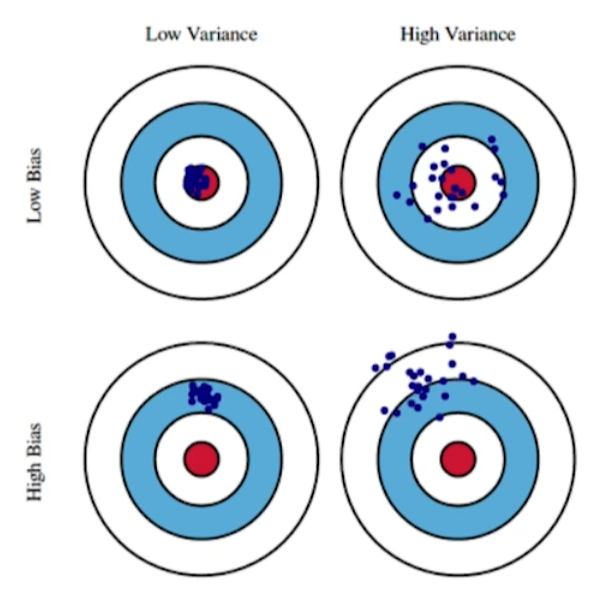ref : https://work.caltech.edu/telecourse

탄착군이랑 똑같이 생각하자. Variance

  • 입력에 대해 출력이 얼마나 일관적인지를 의미.
  • 낮을수록 일관적이다.
  • 높을수록 일관적이지 않다.

Bias

  • 원하고자 하는 값과 얼마나 떨어져 있는지

Bias and Variance Tradeoff

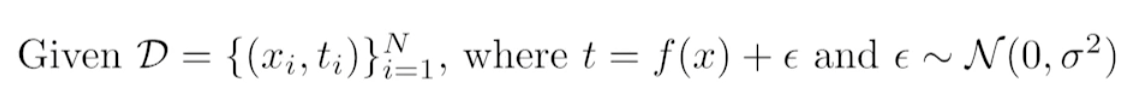학습 데이터에 노이즈가 끼어 있다고 가정할 한다. We can derive that what we are minimizing(cost) can be decomposed into three different parts: \(bias^2\), \(variance\), and \(noise\).

즉, 내가 minimize하는 값은 한가지 값이지만 그 값은 3가지 component이다. 또한 3가지 component는 무언가가 작아지면, 무언가가 커지는 trade-off 관계이다.

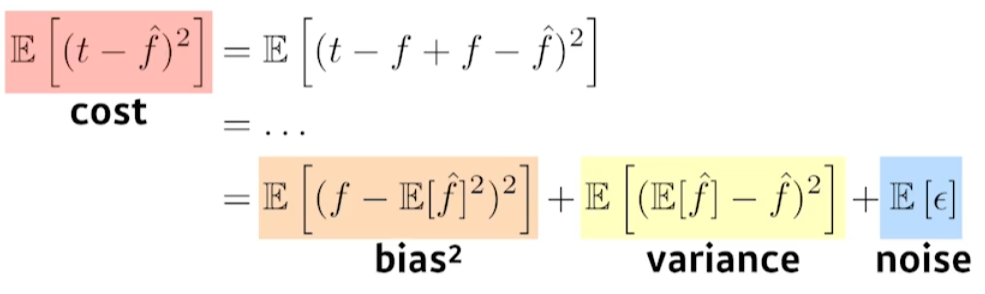
즉, cost를 위와 같이 3가지 term으로 구분해서 생각할 수 있는 것이다. 보통 bias와 variance가 trade-off라고 한다.

Bootstrapping

통계학에서 사용되는 용어. Bootstrapping is any test or metric that uses random sampling with replacement.

가령 100개의 학습데이터에 대해서 무작위로 80개씩 추출하는 행위를 통해 여러 개의 모델 configuration을 만들어 서로 비교할 때 사용한다.

Bagging, Boosting

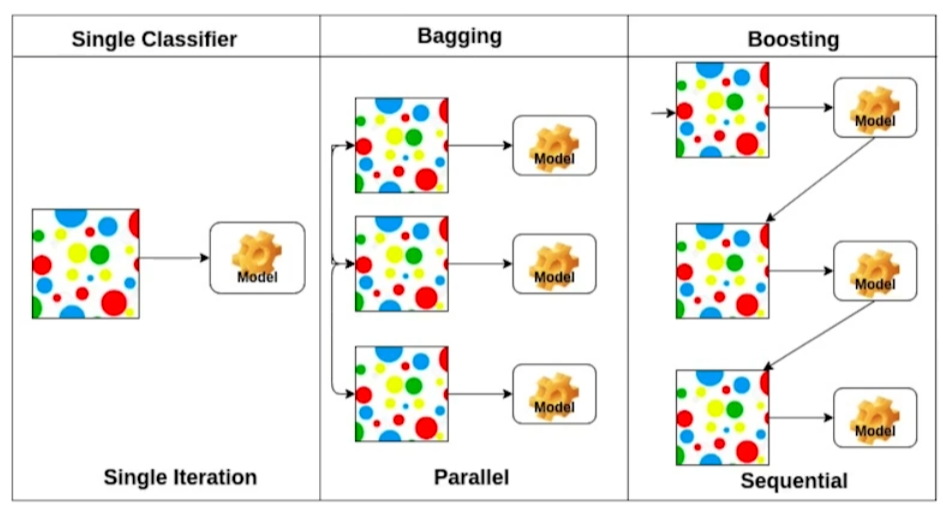
Bagging(Boostrapping aggregating)

  • eg. Bootstrapping을 통해 학습 데이터를 여러개로 subsampling한다. 여러개의 학습 데이터별로 서로 다른 모델의 output이 발생하고 이를 활용한다. (통계값을 추출하거나 앙상블 학습을 하거나 등등)

전체 학습 데이터를 하나의 모델에 대해 한번만 학습해 하나의 결과를 추출하는 것보다 더 좋은 성능을 보여주는 경우가 대부분이다. Kaggle같은 대회에서 대표적으로 사용되는 기법이다.

Boosting 가령 학습을 할 때, 80개의 데이터에 대해서는 분류가 잘 되지만 나머지 20개의 데이터에 대해서는 분류가 잘 안된다고 가정해보자. 나머지 20개에 대해서는 별도의 모델을 생성해서 학습을 한다. 이러한 방식으로 만들어진 모델을 weak learner라고 하자.

이러한 weak learners를 sequence하게 묶어서 하나의 strong learner를 만든다. boosting에서는 weak learner들의 weight들을 sequence하게 학습한다.

Practical Gradient Descent Method

  • Stochastic gradient descent
    • 한번에 하나의 데이터만을 사용해 parameter 업데이트.
  • mini-batch gradient descent
    • 한번에 subset 데이터만을 사용해 parameter 업데이트.
  • batch gradient descent
    • 모든 데이터를 한번에 활용

Batch size matters

We .. present numerical evidence that supports the view that large batch methods tend to converge to sharp minimizers of the training and testing functions. In constrast, small-batch methods consistently converge to flat minimizers… this is due to the inherent noise in the gradient estimation.

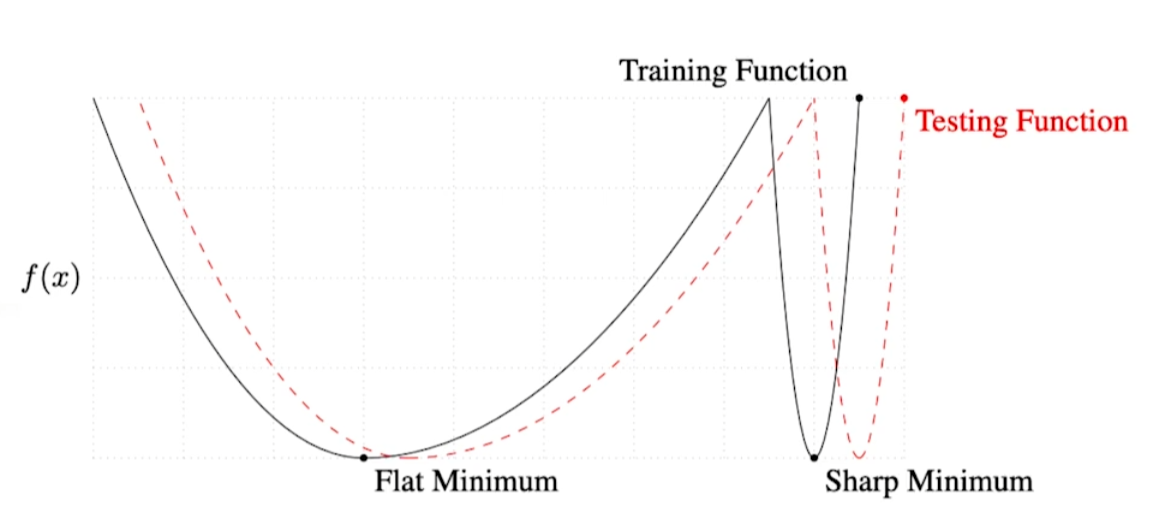
해당 논문에서 large batch method는 sharp minimizer를, small-batch method는 flat minimizer를 가진다고 한다. 이에 대한 설명은 아래 그래프와 같다.

ref: https://arxiv.org/pdf/1609.04836.pdf (ON LARGE-BATCH TRAINING FOR DEEP LEARNING: GENERALIZATION GAP AND SHARP MINIMA)

flat minimum : test function과 training function이 멀더라도, 어느정도 학습이 된다. Generalization performance가 높다! sharp minimum : Geenralization performance가 낮다.

Gradient descent methods

(Stochastic) Gradient descent

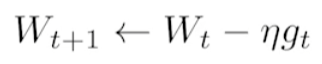너무나도 익숙한 기본적인 Gradient descent의 parameter update 수식이다.

문제점 : η(learning rate)를 잡는 것이 어렵다. 너무 작으면 학습 진행이 안되고, 너무 크면 학습이 제대로 안된다.

Momentum

말 그대로 Momentum(관성)을 유지하면서 parameter를 업데이트한다. β(momentum)은 hyper parameter이다. β와 gradient, 이전 step의 accumulation을 통해 새로운 accumulation을 얻는다. 이를 통해 이전 step에서 사용된 정보를 SGD처럼 모두 버리지 않고, 어느 정도 유지하면서 W를 업데이트한다.

Nesterov Accelerated Gradient(NAG)

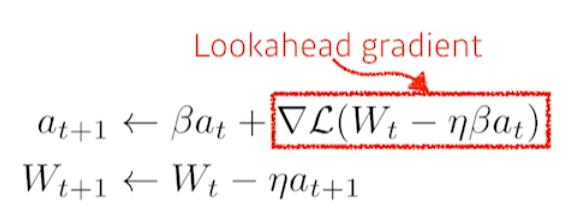
수식의 큰 틀은 momentum과 같다. 다른 점은 다음 스텝의 graident를 미리 계산해보고 이렇게 계산된 Lookahead gradient를 활용해 accumulation을 업데이트한다.

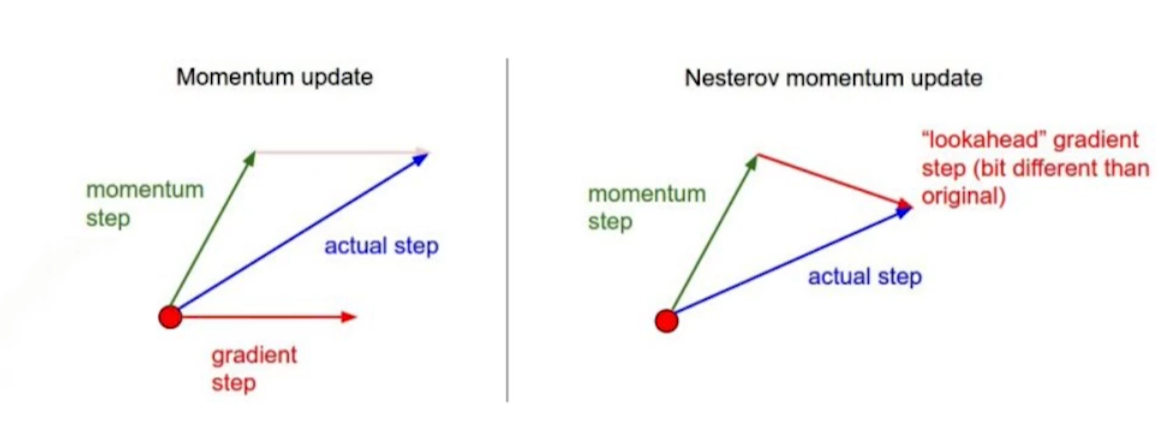
ref: https://golden.com/wiki/Nesterov_momentum

Moementum과 Nesterov momentum은 위 그림과 같은 차이가 있다. 직관적으로 이해해보면, momentum은 converge point에 한번에 수렴하지 못하고 진자마냥 움직이면서 수렴을 하지 못하는 경우가 생긴다.

Nesterov는 다음 step의 gradient를 활용해 업데이트하기 때문에, 한쪽 방향으로만 가는 효과가 있다. 따라서 NAG가 보통 좀더 빨리 converge한다.

Adagrad

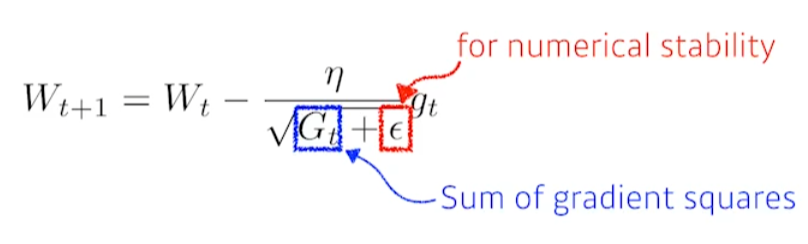
parameter가 지금까지 얼마나 많이 변화했는지를 업데이트에 반영한다. \(G_t\)는 sum of gradient squares다. 즉, parameter가 많이 변화했으면 \(G_t\)가 커지므로 parameter는 적게 변화한다. parametert가 적게 변화했으면 \(G_t\)가 작으므로 parameter는 크게 변화한다.

\(\epsilon\)은 zero division을 방지하기 위해 들어갔다.

문제점 \(G_t\)가 무한정 커질 수 있다. 즉, 분모가 무한대가 되면서 해당 항이 0에 수렴하게 된다. parameter가 더 이상 업데이트 되지 않는 문제점이 발생한다.

Adadelta

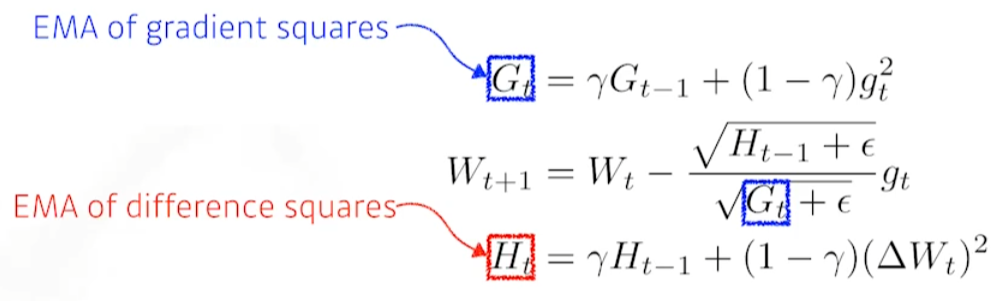
Window size만큼의 시간동안 gradient의 변화만을 보는 방법론이다.

문제는 \(g_t\)의 parameter가 모델의 parameter 개수만큼 존재해야하는 것이다. model의 parameter는 개별적으로 하나의 gradient를 가지기 때문이다. 그렇다면 GPT3와 같은 대형모델에서 천억개의 parameter를 가진다고 하면, \(g_t\) 또한 천억개의 parameter에 대한 gradient정보를 windows size만큼 가지고 있어야한다.

이를 해결하기 위해 exponential moving average(EMA, 이동평균)을 사용한다. 위 수식에서 \(\gamma\)를 사용한 방식이라고 한다…(?)

learning rate가 없다! = hyper parameter를 변경할 수 있는 여지가 없다. 따라서 실용적으로 활용되지는 않는다.

RMSprop

논문으로 발표된 방식은 아니고, Geoff Hinton이 강의 중에 공개한 optimzation. 실제로 논문들이 RMSprop을 사용할 때, Geoff Hinton의 lecture link를 citation했다고 한다.

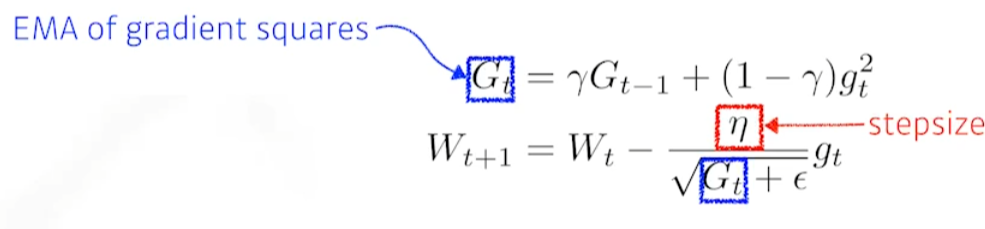
Adam(Adaptive Moment Estimation)

past graidents(momentum)과 squared gradients(Adagrad, RMSprop…)을 합친 것. 즉, momentum 정보와 adaptive learning rate 방식을 혼용한 것.

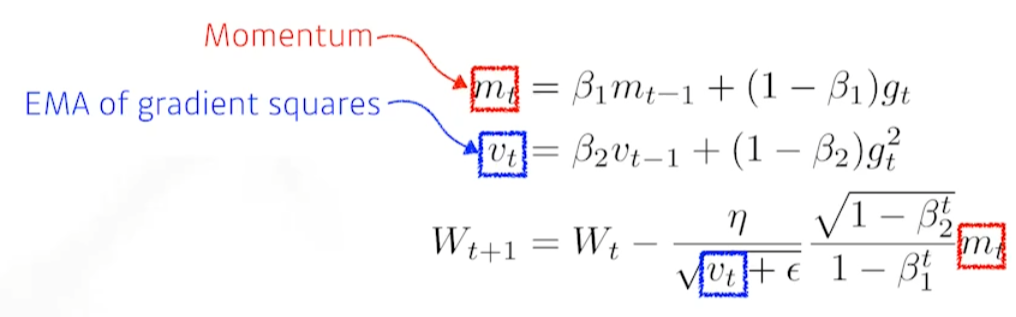
4개의 hyper paramter를 조정하는 것도 매우매우 중요하다.

  • \(\epsilon\) : 매우 작은 값
  • \(\beta_1\) : momentum
  • \(\beta_2\) : graident squares
  • \(\eta\) : learning rate

Regularization

학습을 규제, 방해해서 학습데이터에서만 모델이 잘 작동하는 것이 아니라, 테스트 데이터에서도 잘 작동하도록 하는 것이 목적.

Early stopping

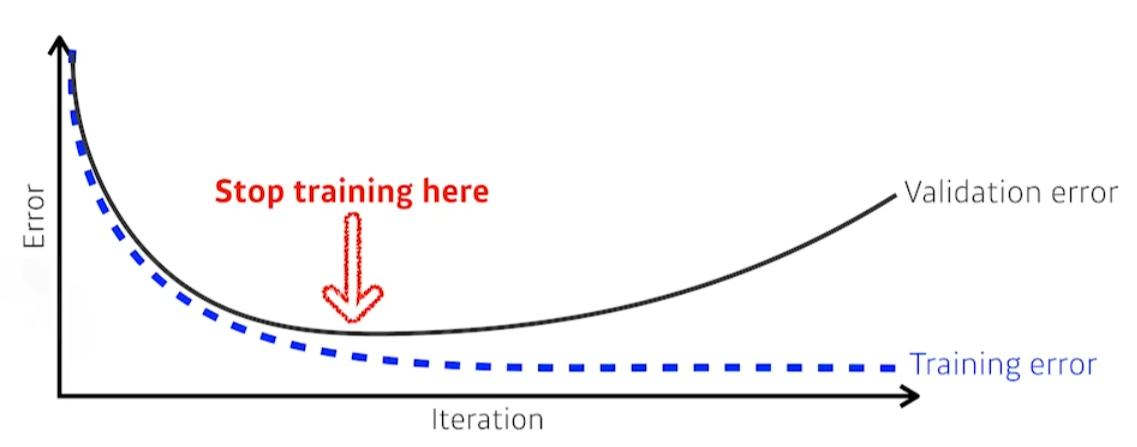test data가 아닌 validation data를 활용해, 적절하게 멈추는 시점을 정한다.

Parameter Norm Penalty

parameter의 크기가 커지지 않게 하는 것.

total cost를 작게 하는 방향으로 학습하자.

함수 공간 내에서 함수를 되도록 부드럽게 만들자.(?) 라고 강사님이 말씀하셨는데 무슨 말인지 모르겠다..

parameter norm penalty를 weight decay라고 부르기도 한다.

Data Augmentation

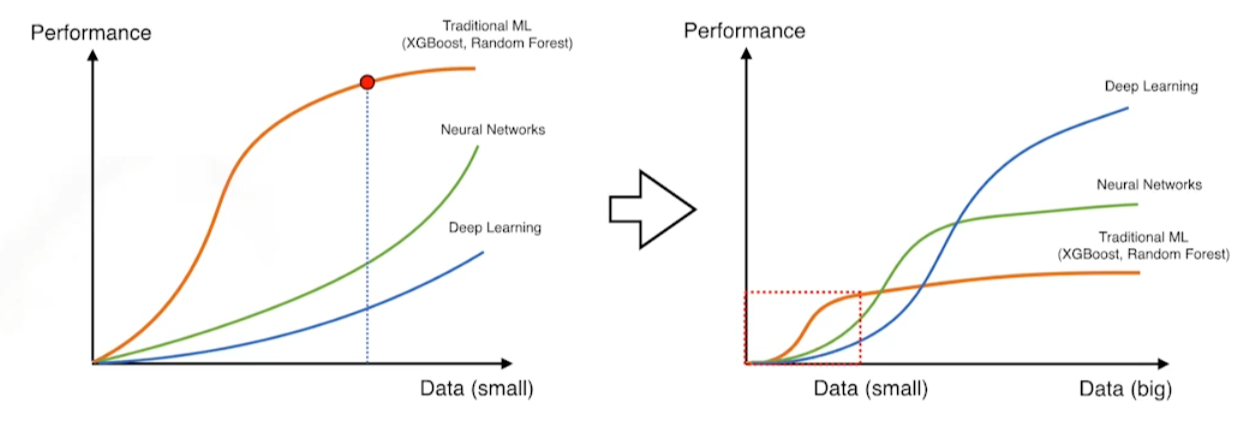DL, NN은 전통적인 ML과 다르게 데이터가 많으면 많을수록 좋다. 그래서 이미지를 뻥튀기하듯이 데이터를 많이 생성하면 되도록 좋다.

위 그림과 같이 이미지의 크기, 기울기, crop 정도를 변화하면서 data를 늘린다. 단, 라벨은 고정되어야한다.

Noise Robustness

입력 데이터와 weight에 noise를 넣어주어 학습하면 테스트 단계에서 더욱 잘 작동한다. 완벽하게 증명은 안됐지만, 실험적으로는 증명됨.

Label Smoothing

학습 단계에서 학습 데이터 두 개를 추출해 섞어서 새로운 학습 데이터를 생성. Decision boundary를 부드럽게 만들어주는 효과가 있다고 한다.

모델의 성능을 매우매우 잘 올릴 수 있는 방법론이다!

ref: https://arxiv.org/pdf/1905.04899.pdf (CutMix: Regularization Strategy to Train Strong Classifiers with Localizable Features)

Mixup : 두 개의 이미지와 라벨을 섞는다. Cutout : 이미지의 일정 부분을 제거 CutMix : Mixup과 다르게 잘라서 섞는다.

Dropout

랜덤하게 일부 뉴런을 0으로 만들어준다. 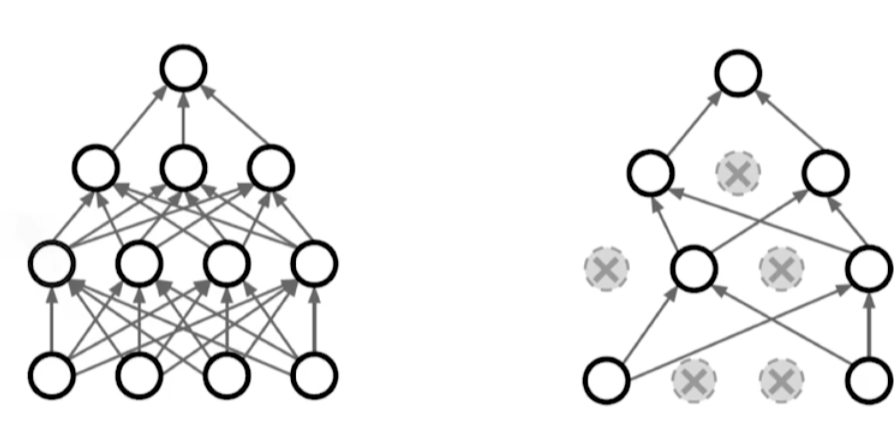뉴런들이 좀더 robust한 feature를 가진다고 해석한다. 이 또한 증명은 없다.

Batch Normalization

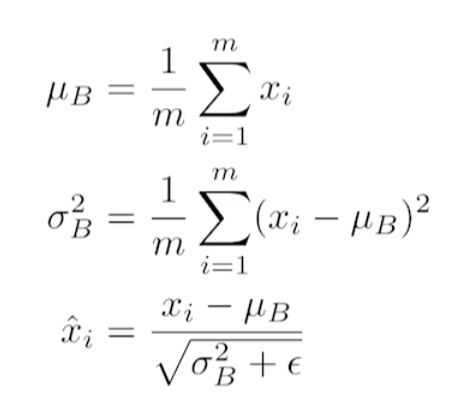
layer별로 weight들의 mean과 variance를 활용해 weight를 normalize한다. 위 수식처럼 mean을 빼고 variance로 나눠줘서 새로운 weight를 구한다.

논문에서는 이러한 행위가 Internal covariate shift를 줄이기에 성능이 향상된다고 해석했는데, 여러 반박 논문들이 있다고 한다..

확실한 것은 BN을 사용하면 Network가 깊어질수록 사용하지 않을 때보다 성능이 많이 좋아진다.

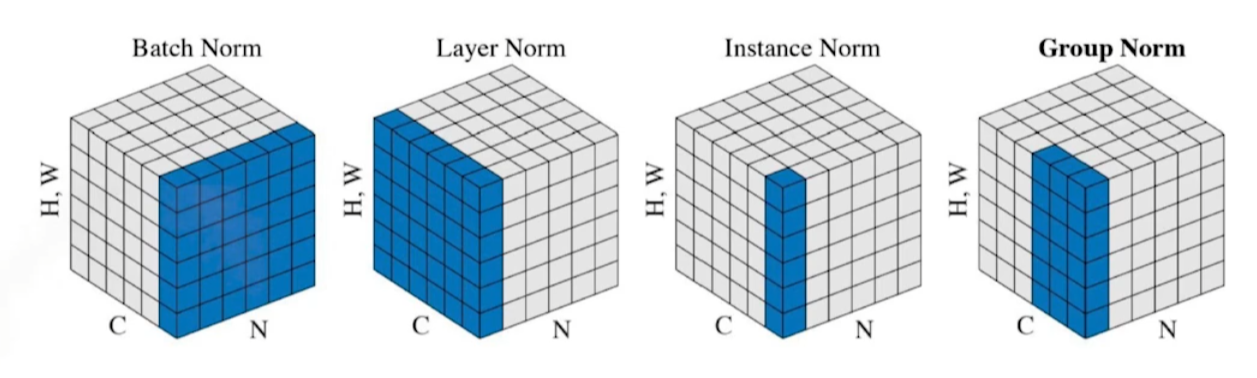
BN과 비슷한 방법론들이 있다. 적절하게 사용하자.

Leave a comment

You may also enjoy