RNN
RNN
시퀸스 데이터(sequence)
- 소리, 문자열, 주가 등 순차적으로 진행되어야 하는 데이터.
- 독립동등분포(iid, independent and identically distributed)를 위배하기 쉽다.
- 가령, ‘개가 사람을 물었다’와 ‘사람이 개를 물었다’는 데이터 분포, 빈도, 의미 등 모든 것이 바뀐다.
- 순서를 바꾸거나 과거 정보에 손실이 발생하면 데이터의 확률분포가 달라진다.
- 과거의 정보 또는 맥락 없이 미래를 예측하는 것은 불가능하다.
시퀸스 데이터 다루기
이전 시퀸스의 정보를 통해 앞으로 발생할 데이터의 확률분포를 다루기 위해 _조건부확률_을 이용.
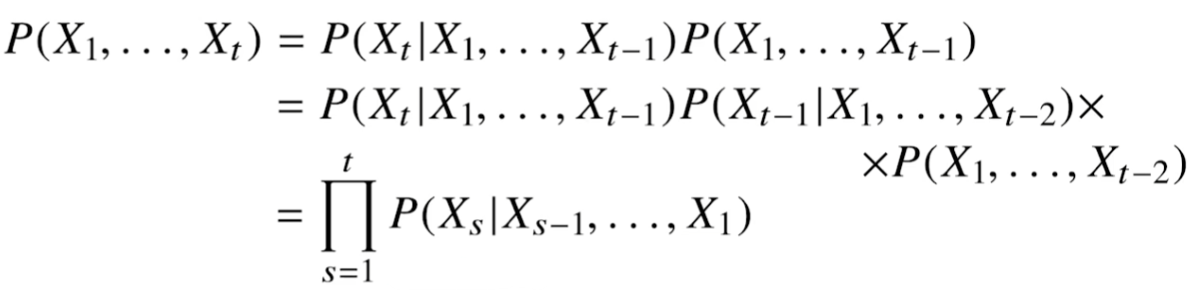
모든 과거의 정보들을 활용해서 조건부확률을 계산하고자한다면 위와 같이 식을 세울 수 있다.
보통은 아래와 같이 시퀸스 데이터를 다룬다.
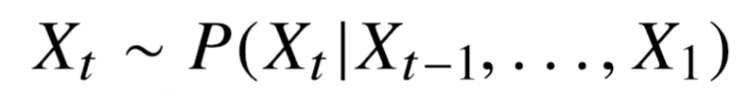
즉, 과거의 모든 정보가 필요한 것은 아니다. 물론 도메인에 따라 천차만별이다.
가령 주가를 예측하는데 30년 전에 창업된 기업의 창업일부터 현재까지의 모든 정보를 활용할 필요는 없다. 보통 5년가량의 정보를 가져와 다룬다.
=> 정보를 truncation하는 것도 기술이다.
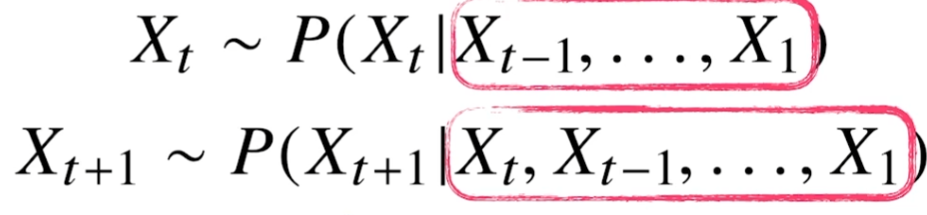시퀸스 데이터는 위와 같이 가변적으로 다룰 수 있어야 한다. 즉, 가변적 길이를 처리할 수 있는 모델이 필요하다.
Autogressive model
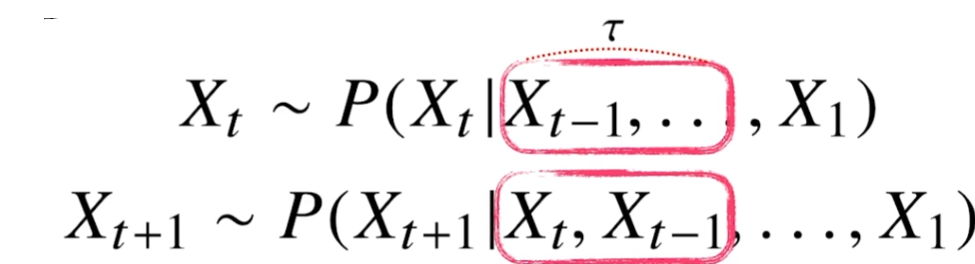τ만큼의 고정된 길이의 시퀸스만을 사용하는 경우도 있다. 이러한 경우를 AR(τ)(Autoregressive model)이라고 한다.
- τ를 결정하는 것조차도 많은 사전 지식이 필요하다
- 필요에 따라 짧고 긴 τ를 정해야한다.
잠재자기회귀모델
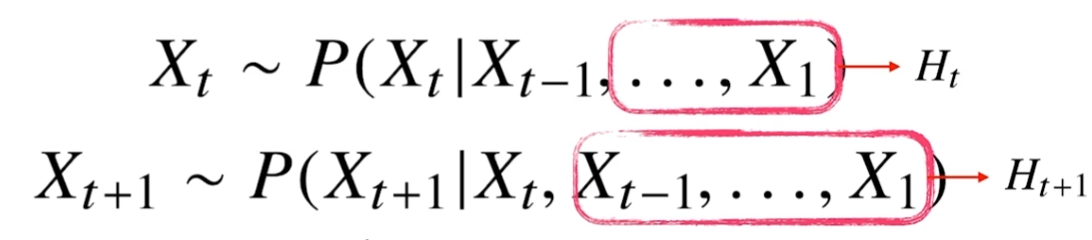
- Xt를 예측할 때, Xt-1과 Ht를 사용해서 예측한다.
- Ht(잠재변수)는 Xt-2부터 X1까지의 정보들이다.
- 가변적인 데이터를 고정적인 데이터로 바꿨다. 모델에서 처리하기 편해진다!
- 문제점 : Ht를 어떻게 인코딩할 것인가?
RNN(Recurrent neural network)
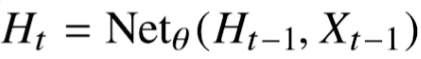잠재자기회귀모델에서의 잠재변수 Ht를 신경망을 통해 반복사용하여, 시퀸스 데이터의 패턴을 학습하는 모델.
네트워클을 수식화하면 아래와 같다.
- Xt : 현재 시점의 시퀸스 데이터
- Ht : 현재 시점까지의 잠재변수
- W(1), W(2) : 시퀸스 데이터의 시점에 관계없이 모든 시퀸스 데이터에 사용되는 가중치 행렬들.
이러한 네트워크는 현재 시점의 시퀸스 데이터만을 다룰 수 있다. 따라서 아래와 같이 네트워크를 확장해본다.
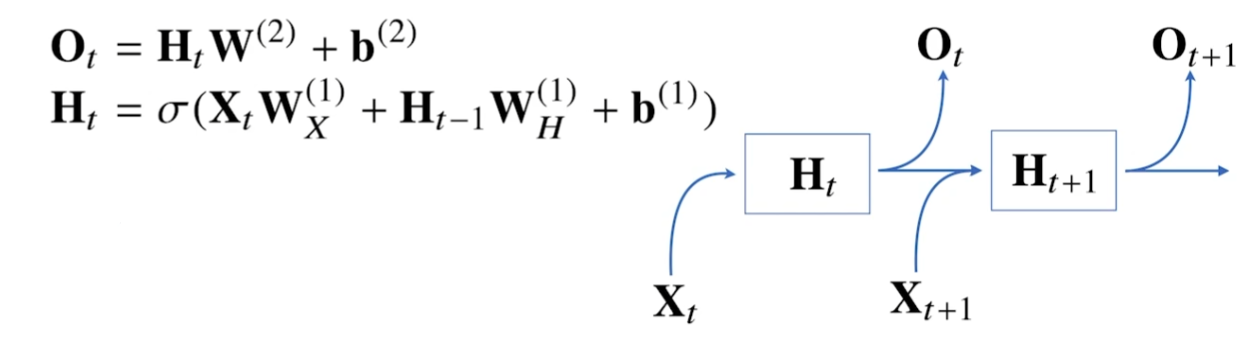
- Wx(1) : 현재 시점의 시퀸스 데이터로와 결합되는 가중치 행렬
- WH(1) : 이전 시점의 잠재변수와 결합되는 가중치 행렬
- Ht : 새롭게 계산된 잠재변수. 복제되서 다음 순서의 잠재변수를 인코딩하는데 사용.
- 전체 네트워크에서 사용되는 고정된 가중치 행렬 : Wx(1), WH(1), W(2)
BPTT(Backpropagation through time)
RNN의 역전파 방법
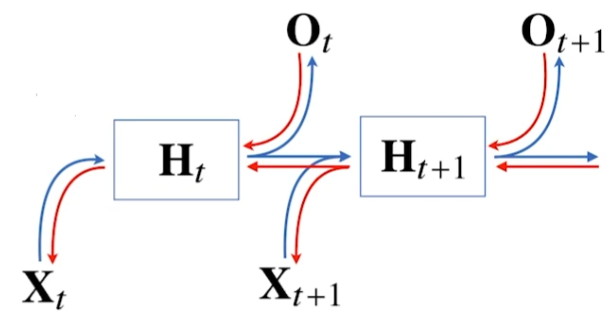
- 빨간색 : gradient의 전달 경로
- 파란색 : foward propagation
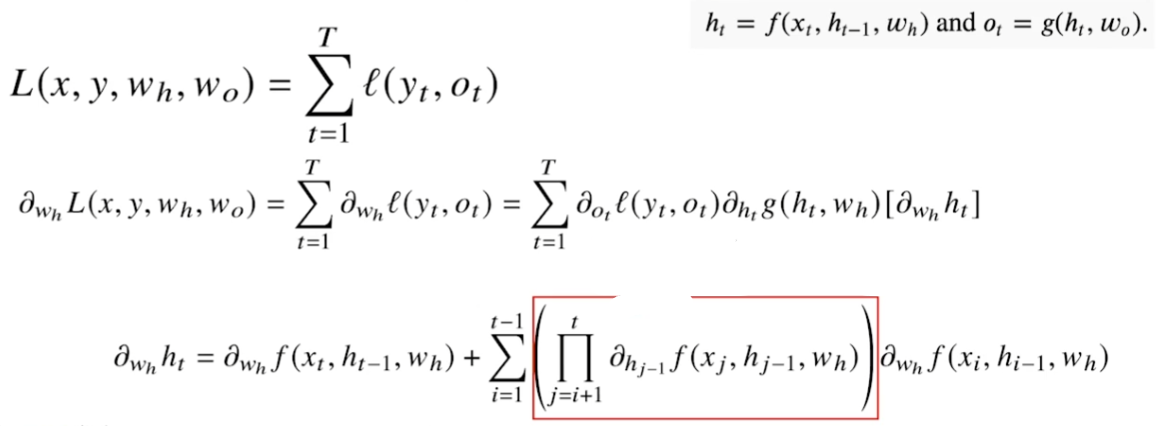시퀸스 길이가 길어질수록 빨간색 박스 내의 항은 불안정해지기 쉽다. 해당 박스 내의 값이 0보다 작다면 값이 매우 작아지고, 0보다 크다면 값이 매우 커진다.
Truncated BPTT
모든 시퀸스 순서에 대해서 gradient를 모두 계산한다면 위에서 봤듯이 미분항이 매우 불안정해지면서 기울시 소실(gradient vanished)가 발생한다.
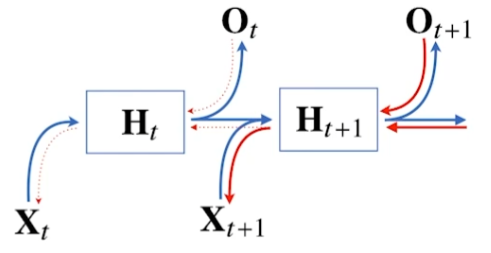
따라서 적절히 끊어준다.
가령 위 그림에서는 정상적으로 BPTT를 하다가, Ht에 대해서는 Ot에서만 graident 정보를 받아서 graident를 업데이트한다.
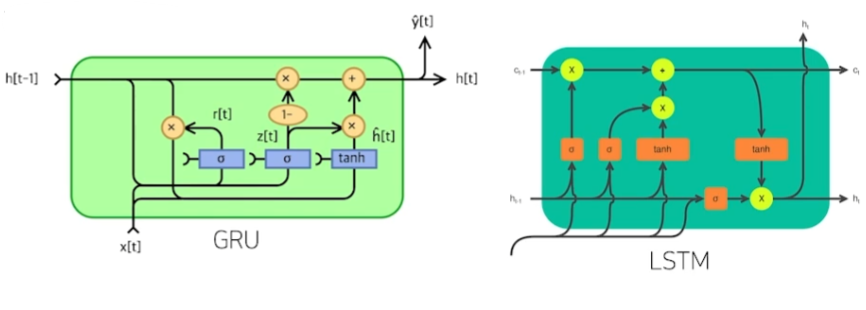
하지만 이조차도 한계가 있기 때문에 LSTM과 GRU를 통해 이를 해결한다.
Leave a comment