확률론

작년에 lieklihood 관련해서 정리하면서도 이해가 잘 되지 않았던 내용들이다. 부캠 내용들 위주로 다시 재정리했다.

확률론

딥러닝은 확률론 기반의 기계학습 이론이 바탕이다.

확률분포

데이터 공간 (X x y)에서 확률분포 D는 데이터 공간에서 데이터를 추출하는 분포.

이 때, y가 상정됐기 때문에 정답 레이블이 있는 지도 학습을 기준으로 설명한다.

확률 변수

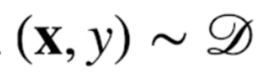확률 변수 = 데이터 공간 상의 관찰 가능한 데이터.

• 데이터를 추출할 때 확률 변수를 사용.
• 확률분포는 확률변수를 추출한 분포를 의미.

확률 변수의 종류

확률변수는 확률분포 D에 따라 discrete와 continuous로 구분된다.

데이터 공간에 따라 구분되는 것이 아니다. 가령, 정수 공간의 확률 변수는 필연적으로 이산형이다. 하지만 실수 공간의 확류 변수라도 -0.5와 0.5만 선택 가능하다면 이산형이다.

이산확률변수(discrete)

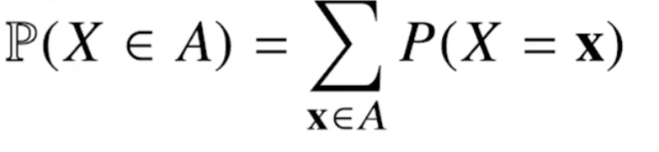확률 변수가 가질 수 있는 경우의 수를 모두 고려한 확률의 합으로 모델링. 확률질량함수라고 부른다.

연속확률변수(continuous)

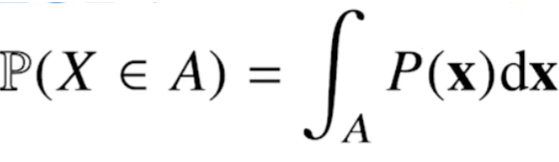데이터 공간에 정의된 확률변수의 밀도를 적분하여 모델링.

이 때, 밀도는 다음과 같다.

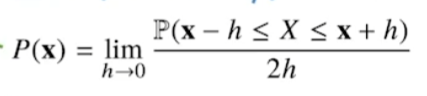
밀도는 누적확률분포의 변화율로 확률이 아니다!

결합분포(Joint distribution)

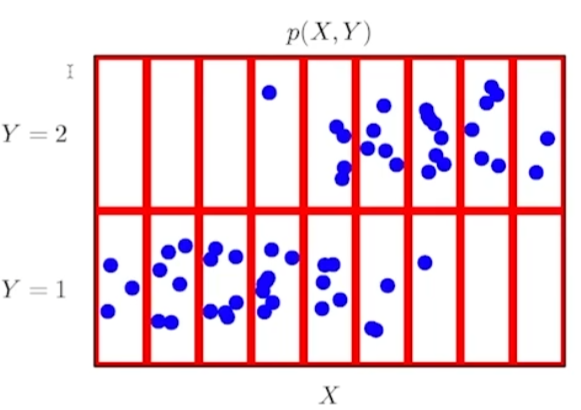
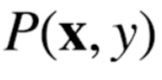전체 데이터 X, y가 주어진 상황에서 분포를 상정할 수 있는데 이러한 분포를 결합분포(Joint distribution)라고 한다. 결합분포는 확률분포 D를 모델링한다.

위 그림에서 실제 데이터들은 파란색 점이다. 연속확률변수처럼 보이지만, 결합분포를 빨간색 박스처럼 상정하면 마치 이산확률변수처럼 다룰 수 있다.

이 때, 실제 데이터의 분포의 종류와 결합 분포의 종류는 무관하다. 모델링하기 나름이다.

왜냐하면 컴퓨터로 데이터를 다루기 때문에, 원래 확률분포 D를 근사하기 위해 결합분포 P(X, y)는 적절하게만 설정하면 무방하다.

주변확률분포(Marginal probability distribution)

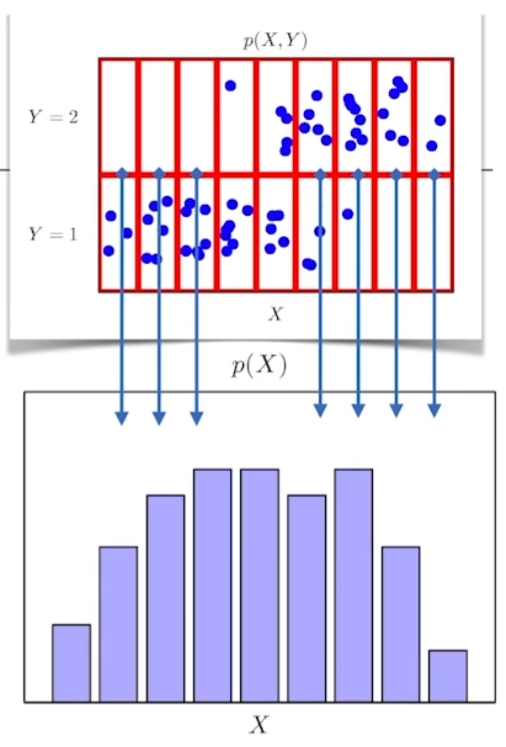
P(x) = 입력 x에 대한 주변확률분포, y에 대한 정보는 없다. 위 그림처럼 x에 대한 수를 셀 수도 있고 적분을 한 정보를 줄 수도 있다.

반대로 y에 대한 주변확률 분포도 상정 가능하다. 즉, y에 대한 수를 세거나 적분을 한 P(y)를 정의하는 것이다.

조건부확률분포

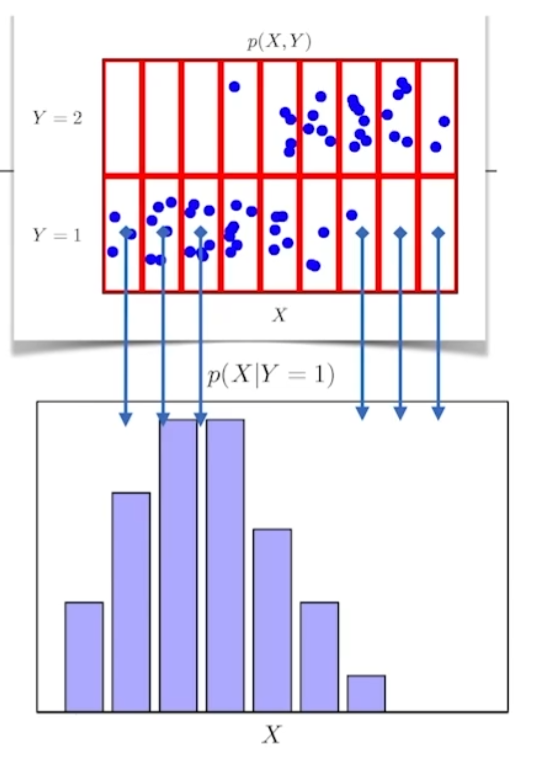P(x|y) = 입력 x와 출력 y 사이의 관계를 모델링 위 그림처럼, 조건부확률분포는 y=1일 때의 x의 정보를 모델링할 수 있다.

조건부확률과 기계학습

P(y|x) = 입력변수 x에 대해 정답이 y일 확률

Logistic Regression에서 선형모델과 softmax의 결합은 데이터에서 추출된 패턴을 기반으로 확률을 해석하는데 사용한다.

조건부확률 P(y|x)를 구하는 방법

• 분류 문제에서 softmax(WΦ + b)는 데이터 x로부터 추출된 특징패턴 Φ(x)과 가중치 행렬 W를 통해 계산

• P(y

  x) 대신 P(y

  Φ(x))라 해도 무방.

딥러닝

• NN을 통해 데이터로부터 특징패턴 Φ를 추출.

기대값

확률 분포가 주어진 데이터를 분석할 때, 여러 통계적 범함수(statistical functional)을 계산할 수 있다.

이 때, 기대값(expection)은 데이터를 대표하는 통계량이다. 평균(mean)이다. 또한 확률분포를 통해 다른 통계적 범함수를 계산하는데 사용된다.

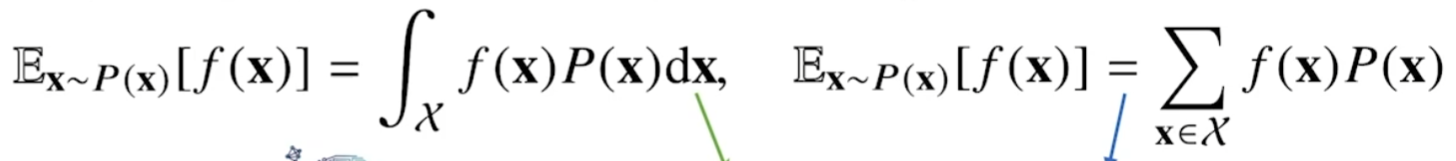
연속활률분포에서는 적분으로, 이산확률분포에서는 급수로 계산한다.

용례

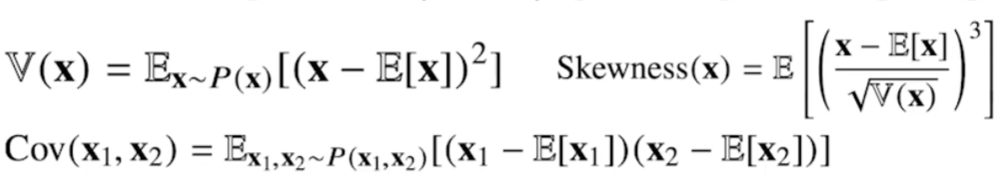분산, 첨도, 공분산 등을 계산할 때 사용한다.

회귀 문제의 조건부기대값 추정

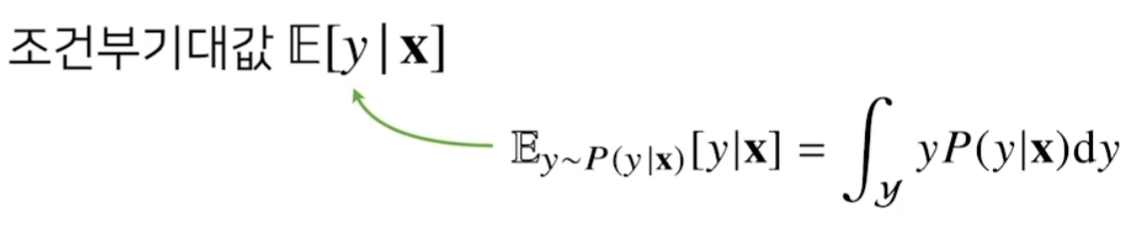조건부기대값은 L2 norm을 최소화하는 함수와 일치한다.

회귀문제에서 robust(강건)하게 추정하는 경우, 조건부기대값보다는 median을 사용.

몬테카를로(Monte carlo) 샘플링

대부분의 기계학습 문제들은 확률분포를 모르는 상태로 문제풀이를 시작하게 된다.

즉, 데이터만을 이용하여 기대값을 계산해야되는데 이 때 사용되는 것이 몬테카를로 샘플링이다.

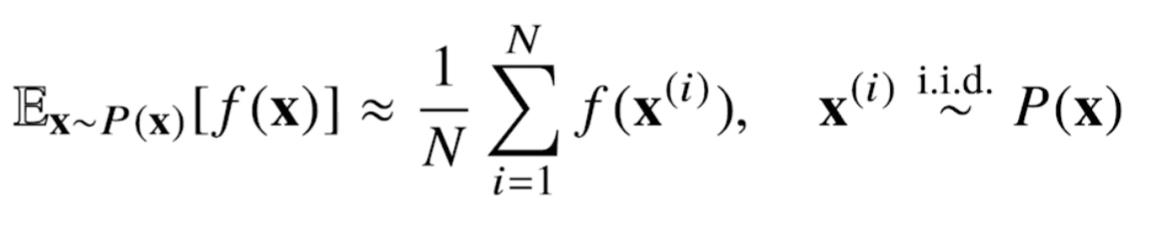
수식 설명

1. f에 샘플링한 데이터 x를 대입한다.
2. 샘플링한 데이터들의 산술평균을 계산한다.
3. 2번의 값이 기대값에 근사하게 된다.

몬테카를로는 이산형이든, 연속형이든 상관없이 사용 가능하다.

몬테카를로 샘플링은 독립추출이 보장되어야 한다.

• 대수의 법칙(law of large number)에 의해 수렴성 보장.

몬테카를로 샘플링 예시

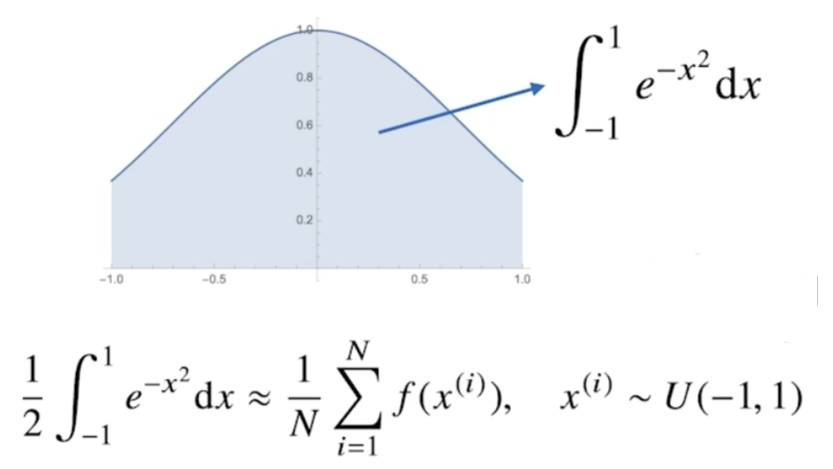
위 함수를 [-1, 1]에서 적분하는 것은 해석적으로 불가능하다. 이럴 때, 몬테카를로 샘플링을 사용한다.

1. 함수의 적분식을 마치 몬테카를로 샘플링처럼 구성하기 위해 함수의 적분 수식에 2를 나눠준다. 왜냐하면 적분에서는 성분의 개수라는 것을 상정할 수 없기 때문에, 적분하고자 하는 x의 범위의 길이를 마치 성분의 개수처럼 사용하느 것이다.
2. [-1, 1]에서 균등분포로 N개의 데이터를 추출하여 산술평균을 구한다.

def mc_int(fun, low, high, sample_size=100, repeate=10):
    int_len = np.abs(high - low)
    stat = []
    for _ in range(repeat):
    	x = np.random.uniform(low=low, high=high, size=sample_size)
        fun_x = fun(x)
        int_val = int_len * np.mean(fun_x)
        stat.append(int_val)
    return np.mean(stat), np.std(stat)
def f_x(x):
    return np.exp(-x**2)
    
print(mc_int(f_x, low=-1, high=1, sample_size=10000, repeat=100))