Bag-of-Words
Bag-of-Words
딥러닝 이전에 단어를 숫자로 나타내는 기법.
Bag-of-Words Representation
1. Constructing the vocabulary conatining unique words.
여러 문장에 걸쳐 중복되게 사용된 단어라도 Vocabulary에서는 한번만 표현된다.
2. Encoding unique words to one-hot vectors.
Vocabulary에 존재하는 단어들을 일종의 categorical data로 볼 수 있어서 one-hot vecotr로 표기해보는 것.
가령, Vocabulary에 8개의 단어가 있다면 8차원의 one-hot vector를 구성하는 것이다.
For any pair of words, the Euclid distance is $\surd2$.
For any pair of words, the cosine similarity is 0. 모든 내적의 조합이 0이니까.
즉, 단어의 의미에 관계없이 모든 단어가 동일한 관계를 가진 형태로 벡터를 표현한다.
Bag-of-words vector
One-hot vector로 단어들을 표현했다면 문장을 one-hot vecotr로도 표현 가능하다.
즉, 문장을 모든 단어들의 one-hot vector의 합으로 나타내는 것인데 이것이 Bag-of-Words vector다.
NaiveBayes Classifier
문장이나 문서를 Bag-of-words vector로 표현했을 때, 해당 vector를 특정 category로 분류하는 방법론.
d: document
c: class
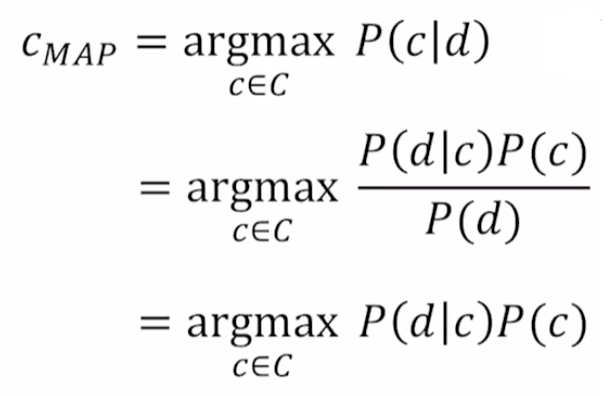
- P of c, given d.
-
MAP: Maximum a posteriori = Most likely class. $P(c d)$에서 가장 높은 확률을 가지는 class c를 선택하는 방법.
-
- Bayes rule에 의해서 두번째 수식으로 변경 가능.
- $P(d)$는 특정 document가 뽑힐 확률로 상수 취급 가능하다. 따라서 무시하면 세번째 수식을 도출할 수 있다.
-
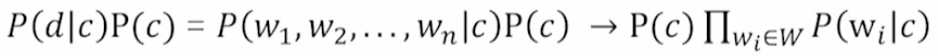
$P(d c)$: category c가 고정됐을 때 문서 d가 나타날 확률. - d는 w1, …, wn까지의 word가 동시에 나타날 사건으로 볼 수 있다.
- 따라서 가장 왼쪽처럼 수식을 변화시킬 수 있다.
| 즉, $P(c)$와 $P(w_i | c)$를 추정할 수 있다면 NaiveBayes classifier에서 원하는 parameter들을 모두 추정할 수 있다. |
적용
-
$P(c)$와 $P(w_i c)$를 모든 경우의 수에 대해서 구해준다. -
새로운 입력에 대해서 1번에서 구한 데이터를 활용해 category별로 $P(c)$와 $P(w_i c)$를 구한다. - argmax를 구한다.
문제점
학습 데이터 상에 존재하지 않는 입력이 들어올 경우, 해당 단어에 대해서는 $P(w_i|c)이 0이 된다. 즉, 다른 단어들이 특정 class와 아주 밀접한 관련이 있음에도 모든 클래스에 대한 확률이 0이 될 수 있다.
=> regularization을 통해 해결한다고 한다.
실제 계산
$P(c)$와 $P(w_i|c)$은 단순히 개수를 세는 것처럼 구할 수도 있지만 실제로는 MLE 등을 활용해 구한다고 한다.
Leave a comment