Beam search
Greedy decoding
이전 포스팅의 attention이나 LSTM들은 특정 step에서 다음 단어를 예측할 때, 가장 확률이 높은 하나의 단어를 선택한다. 이러한 방법을 greedy decoding이라고 한다.
전체적인 맥락에서 예측하는 것이 아니라 근시안적으로 가장 좋은 방법을 택하기 때문이다.
예를 들면 아래와 같다.
input: {어려운 프랑스어}, answer: he hit me with a pie
이러한 상황에서 decoder가 ‘he hit a’까지만 예측했다고 해보자. 분명 틀린 문장이 되버렸지만 greedy decoding에서는 돌이킬 수 있는 방법이 없다.
Exhaustive search
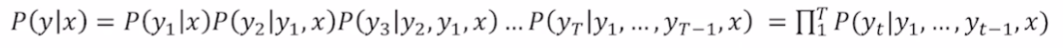Greddy decoding에서 주어진 문장 x에 대한 출력 y는 위와 같은 joint probability로 표현이 가능하다.
joint probability의 첫번째 항은 x가 주어졌을 때 y1을 출력할 확률이다. 2번째 항은 y1과 x가 주어졌을 때 y2를 출력할 확률이다. 즉, 이 모든 값들에 대한 곱은 Seq2Seq에서 출력 y에 대한 확률을 모든 token에 대해서 고려한 동시사건들에 대한 확률이다.
목적 $P(y|x)$를 최대화하는 것이다. 가장 자연스러운 y를 찾는 것이 목적이기 때문이다.
문제점 greedy decoding은 목적을 이루지 못할 수도 있다. $P(y_1|x)$를 최대화하는 선택을 근시안적으로 수행하는 것이 문제다. 이러한 선택 때문에 $P(y_1|x)$ 이후에 등장하는 항들의 값이 작아지며 전체적인 값이 작아질 가능성이 존재하기 때문이다.
해결방법 t 시점에서의 확률값이 작아지더라도 전체적인 값을 올릴 수 있는 선택을 하면된다. t 시점에서 선택 가능한 모든 경우의 수를 계산하면 이를 구현할 수 있을 것이다. decoder의 t 시점에서 선택 가능한 경우의 수, 즉 단어의 수를 $V^t$라고 한다면 Complexity는 $O(V^t)$일 것이다. 너무 큰 complexity다.
Beam search
Greedy search와 모든 경로를 탐색하는 방법론의 절충안이다. $V^t$만큼 탐색하는게 아니라 Vocabulary의 수인 V를 k개로 사용자가 설정해서 탐색해보는 것이다.
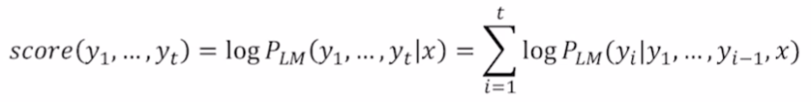k: beam size(in practice around 5 to 10)
하나의 step에서 k개의 hypothesis를 탐색하는 형태다.
기존의 joint probability에 log를 씌워둬서 단조증가함수로 바꿔준다. 즉, 정의역이 커지면 치역도 커지는데 이러한 성질 덕분에 joint probability가 가장 클 때는 log를 취한 score값도 가장 클 것이다. 즉, log 씌워도 무방!
- globally optimal solution을 보장해주지는 못한다.
- exhaustive search보다는 효율적이다!
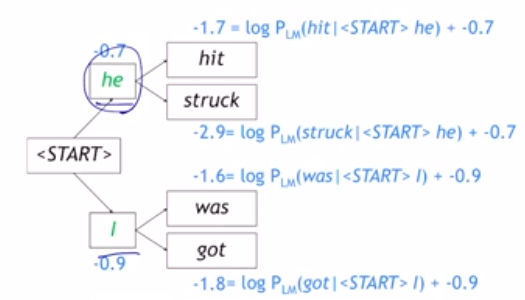hypothesis가 4개로 분할된 양상이다. start에서 k개만큼 hypothesis를 생성한다. 다음 step에서는 각각의 k개에 대해서도 k개의 hypothesis를 분화시킨다. 여기서는 k=2, step=2이므로 hypothesis=$k^n$은 $2^2=4$만큼 분화된다.
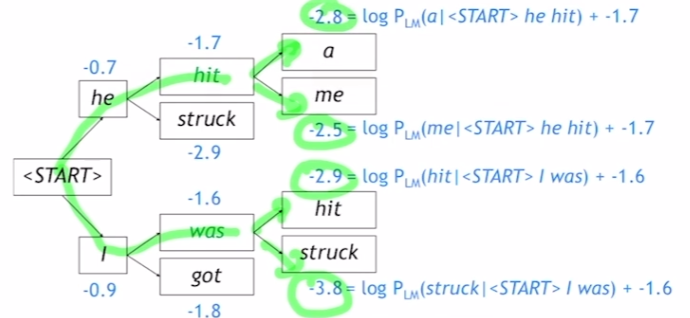하지만 다음 step에서는 k개에 대해서 k개의 hypothesis를 만들지 않는다. 적당히 greedy하게 k개의 hypothesis들 중 확률 값이 가장 큰 것들을 k(2)개 선택한다. 그리고 선택된 hypothesis에 대해서 k개의 hypothesis를 만든다.
이러한 방식을 사용하기 때문에 모든 path를 탐색하는 것보다 훨씬 적은 complextiyr가 소요된다.
Hypothesis 종료조건
Decoder가
## Beam Search 종료조건
- 미리 정해둔 timestep T에 도달했을 때
- 적어도 n개의 hypothesis가 종료됐을 때
최종 평가
확률값이 0과 1사이의 값이기 때문에 joint probability의 길이가 길어질수록 score는 줄어든느 것이 자명하다. log의 값이 음수가 되기 때문이다. 따라서 공평하게 score를 계산하기 위해서 score를 길이로 나눈 값을 score로 사용한다.
Leave a comment