Sungho Park

AI

‘Attention is all you need’(2017) 논문 이전의 attention은 LSTM, GRU에 add-on처럼 쓰일 뿐이었다. 해당 논문에서는 기존의 RNN 모델을 걷어내고 attention을 사용한 새로운 Seq2Seq 모델을 제시했다.

기존의 RNN

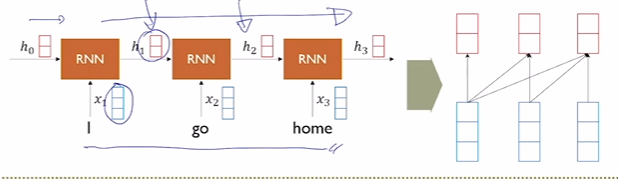
Sequence를 token 단위로 매 step마다 입력으로 받는다. step마다 hidden state를 encoding하여 hidden state를 출력한다. 또한 attention을 사용하여 이전 step의 정보들에 대한 가중치를 부여하는 방식으로 이전 정보들을 현재 step에서 얼만큼 사용할지 정해주기도 했다.

하지만 Sequence의 길이에 비례해서 학습 과정이 길어지는 RNN 특성 때문에 long term dependency, gradient vanishing/exploding과 같은 근본적인 문제점들을 완벽히 해결할 수 없다.

Bi-Directinoal RNNs

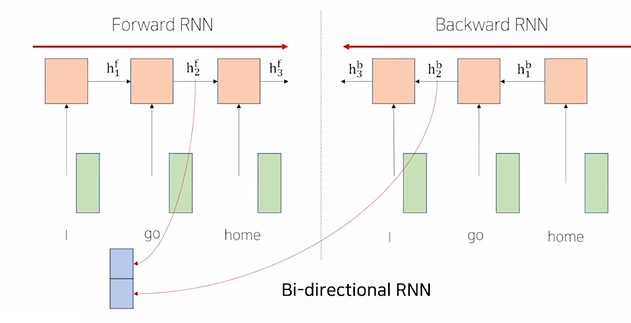기존의 RNN은 다음 step에 대한 정보를 이전 step에서 활용할 수 없다. 위 그림에서 Forward RNN의 경우 ‘I’는 ‘go’, ‘home’에 대한 정보를 알 수 없다. 하지만 순서 상 뒤에 오는 정보를 활용해야 하는 문맥이 분명 존재하기 때문에 Backward RNN이라는 것을 고려할 수 있다.

즉, 기존의 순서를 뒤집이서 병렬적으로 학습을 진행하는 것이다. 위 그림을 에시로 들면 ‘go’에 대해서 $h_2^f$, $h_2^b$라는 두 개의 hidden state를 얻을 수 있다. 이를 단순히 concatenate해서 기존의 hidden state의 2배에 해당하는 크기의 새로운 hidden state를 얻어서 활용할 수 있다.

Transformer

Self-attention

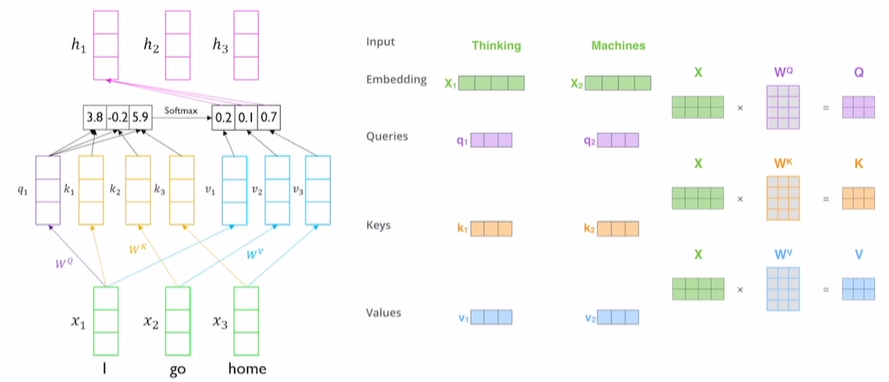(그림1)

transformer에서 input vector가 위와 같이 존재한다고 하자. transformer에서는 sequence의 내용들을 잘 반영하고 input vector의 형식으로 encoding vector를 생성한다.

위 그림을 decoder라고 보자. 그러면 I, go, home이라는 입력을 특정 time step에서 발생하는 decoder의 hidden state라고 볼 수 있다. 동시에 I, go, home을 encoder hidden state vector의 세트라고 볼 수 있다.

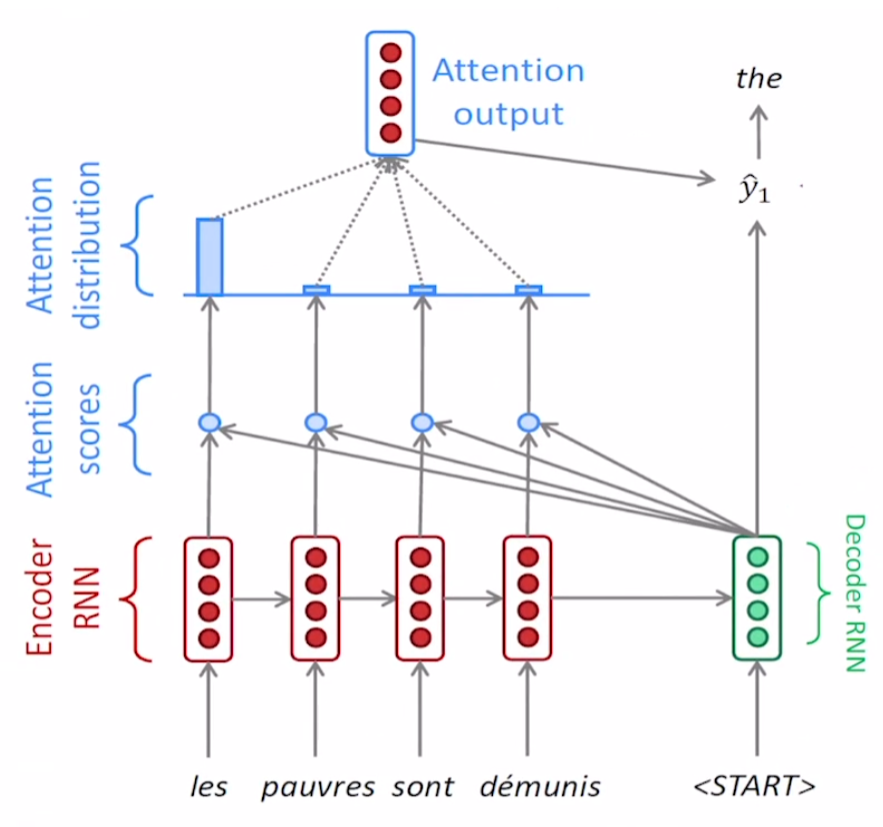이전 attention 포스팅에서 attention을 구할 때 위 그림처럼 encoding의 hidden state과 decoder의 hidden state vector 간의 내적으로 유사도를 구했다.

이러한 과정을 하나의 vector 세트 내에서 수행해서 (그림1)을 self-attentino module이라고 부른다.

문제점

하나의 vector 세트에서 유사도를 측정하기 때문에 자기 자신과의 유사도가 다른 유사도에 비해 매우 크게 나타날 것이다. 즉, output vector는 자기 자신에 대한 정보만을 담고 있는 vector로 구성될 것이다.

우리가 의도하고자 하는 것은 Seq2Seq에서 의도하는 것과 같이 유의미하게 Sequence를 해석해서 결과를 얻어내는 것이지, 자가복제가 아니다.

해결방법

이를 위해서 아래의 세 벡터를 고안한다.

  • Query: 사용하고자 하는 vector set 중에서 어떤 vector를 선별적으로 사용할지 결정해주는 vector다.
  • Key: Query와 어떠한 벡터를 내적해서 유사도를 구해야하는데 이 때 사용되는 재료 벡터.
  • Values: Query와 Key의 내적으로 구해진 가중치가 적용된 벡터.

** Self attention의 구조 ** Self-attention 답게 입력으로 들어온 vector set의 원형을 query, key, values vector로 바꾸는 것이다. 이는 (그림1)에서 보이는 것과 같이 $W^Q$, $W^K$, $W^V$와 같이 서로 다른 linear transform matrix를 통해 각각 선형변환된다.

** Encoding 과정 ** ‘I’를 encoding한다고 해보자.

  1. Q, K, V 연산 $W^Q$를 통해서 Query vector를 만들고, $W^K$를 통해서 Key vector를, $W^V$를 통해서 Values vector를 만든다. 이 때, $k_n$에 의해서 생성된 유사도는 $v_n$에 순서대로 1대1 대응된다.

  2. Attention 가중치 구하기 Q와 K에 대한 유사도를 구하고 이것에 softmax를 취해준다. (그림1)과 같이 자기 자신과의 유사도가 다른 벡터와의 유사도보다 낮음을 볼 수 있다. 자기 자신과의 유사도가 매우 높은 경향으로 높게 측정되지 않는 객관적인 유사도를 얻었다!

  3. Value vector에 Attention 가중치를 적용 ‘I’에 대해 원하고자 하는 encoding vector를 얻는다.

  4. 다음 Seuence에 대해서 동일한 과정 수행 Query만 $W^Q$에 의해 새롭게 연산되고 나머지 Key, Value는 기존에 연산해놨던 결과를 그대로 사용한다.

행렬로 병렬화

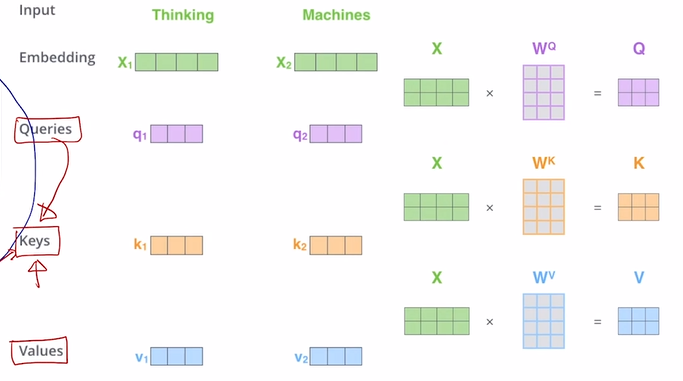
‘Thinking Machines’라는 문장이 있다고 해보자. 이 문장에 대해서 Self attention을 수행하고자 한다면 Q, K, V를 계산해야 한다. 위에서 공부한대로 $X_1$에 해당하는 ‘Thinking’에 대해서 Q, K, V를 구한 후 output vector를 계산한 후 동일 연산을 $X_2$에 적용해도 무방하다.

하지만 행렬로 이를 병렬화해보자.

$X$라는 행렬을 $X_1, X_2$의 concatenate 결과라고 해보자. $X$에 $W^Q$를 dot product하면 이 결과인 $Q$는 $Q_1, Q_2$를 concatenate한 결과와 동일하다. 이는 $K, V$에 대해서도 마찬가지이다.

RNN의 한계를 개선

transformer는 sequence의 길이나, 순서에 무관하게 모든 sequence의 내용들이 Q, K, V로 변환되어 각각의 input vector에 맞는 encoding vector를 만든다. 즉, RNN과 같이 sequnece의 길이가 길어짐에 따라 이전의 정보들을 담기 힘들어지는 hidden state의 근본적인 구조를 탈피했기에 long term dependency의 문제를 상당히 많이 개선했다.

Scaled Dot-Product Attention

  • Input: query $q$, a set of key-value $(k,v)$
  • Q, K, V, Ouput is all vector!
  • Output: weigted sum of values
  • Weigted vector: inner product of query and corresponding key
  • Queries and keys have same dimensionality $d_k$.
  • Dimensionality of value is $d_v$.
  • $d_k$와 $d_v$는 같지 않아도 무방하다!
    • 어차피 values에 대한 가중치 적용은 차원수와 무관하게 벡터 전체에 대한 scalar 곱이다.

일반화

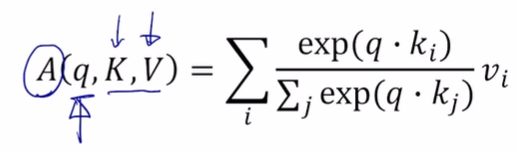
  • i: 몇번째 입력 vector인지
  • j: 모든 입력 vector에 대한 q와 k의 내적을 구하기 위한 index

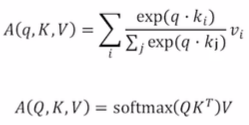
첫번째로 나온 수식은 하나의 query에 대한 self-attention 결과를 나타낸 수식이다. 이를 확장시켜서 Query matrix에 대한 수식을 써보자. 이는 각각의 query를 row로 가지고 있는 matirx다.

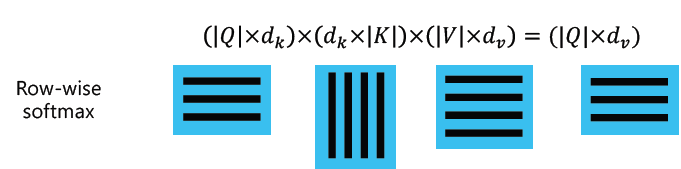
  1. Q와 K 행렬의 곱은 모든 query에 대한 key를 내적해서 softmax를 취하기 이전의 vector들을 row로 가진 matrix를 만들어준다.

  2. Q와 K의 내적 결과에 softmax를 건다. softmax가 matrix에 걸릴 때는, row-wise softmax가 걸리는 것이 기본적이다. 말 그대로 matrix의 row에 대해서 softmax를 취하는 것이다. 즉, 2번의 결과 matrix에는 vector마다 합이 1이 되는 가중치 vector들이 담겨있다.

  3. 2번의 결과와 values matrix를 내적한다. 이 연산에서 의도한 것은 앞서 계속 해왔던 가중치 vector와 values vector의 element-wise 곱 연산을 수행하는 것이다. inner product이기 때문애 가중치들은 column을 따라서 곱해지고 sum이 된다.

여기서 많이 헷갈렸는데 개념을 설명하기 위해서 앞서 설명했던 그림과는 다소 다른 순서로 연산이 진행되어서 그렇다.

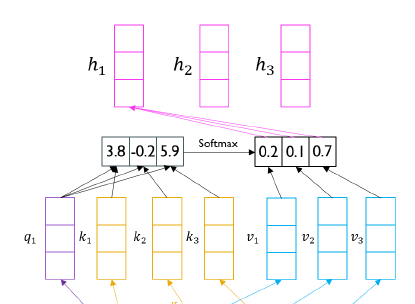
여기서는 0.2라는 가중치는 $v_1$에 scalar 곱이 되고, 0.1은 $v_2$에, 0.7은 $v_3$에 scalar 곱이 되어서 새롭게 변형된 $v_1, v_2, v_3$이 만들어진다. 그 후 이 3개의 벡터들에 대해서 단순 더하기를 수행해 3차원의 vector를 형성한다.

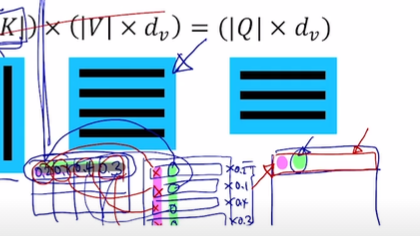
실제 연산에서 사용되는 수식에서는 이미 모든 query에 대한 가중치들이 계산되어 row마다 저장돼있다. 또한 values들도 row마다 하나의 value 벡터를 구성하고 있다. 즉, 단순히 두 matrix를 곱해서 row마다 가중치의 column이 일괄적으로 곱해지고 합해진다.

개념적으로 설명했던 내용들은 행렬을 통해 병렬적으로 계산하고 있다는 이야기다.

transformer 정리

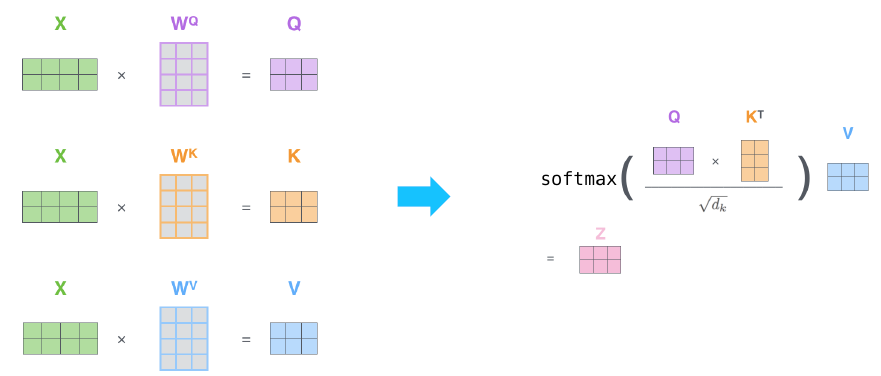scaling 부분만 달라졌을 뿐, 위에서 설명했던 내용들을 모두 정리한 내용이다.

앞서 정리했던 연산 순서를 간략화해보자.

  1. Q, K, V 연산
  2. 위 수식대로 Attention 연산 수행
  3. Encoding vector 얻는다!

이를 도식화하면 아래와 같다.

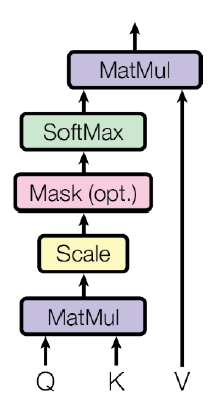
$\sqrt{d_k}$로 scaling하는 이유

조원들끼리 gradient exploding을 방지하기 위해서라고만 이해했다. 물론 이도 어느정도 일리는 있지만 주재걸 교수님 강의에서 논리적인 정답을 찾을 수 있었다.

** 분산 ** 다음과 같이 평균은 0이고 분산이 1인 두 vector를 가정하자.

(a, b), (x, y)

두 vector의 곱은 (x,y)를 transpose해서 $ax+by$로 구할 수 있다.

** 수학적 증명 사실 **

  • 수학적으로 평균이 같은 random variable끼리 곱하면 평균과 분산이 유지된다고 한다.
  • 두 random variable을 더하면 분산 또한 더해진다는 것이 증명됐다고 한다.
  • random variable을 $\sqrt{n}$으로 나누면 random varaible의 분산은 $n$으로 나뉜다.

즉, $ax+by$의 분산은 2가 된다. 여기서는 2차원 vector끼리의 곱을 상정했기 때문에 큰 차이가 나지 않지만, 가령 100차원이었다면 분산은 100이 된다.

분산이 2라면 표준편차는 $\sqrt{2}$이고 가령 이 때의 곱 결과를 $[1.1, -0.8, -1.7]$이라고 하자. 이 값들이 가령 분산이 100이 되버린다면 $[8, -11, 7]$이 되버릴 수도 있다. 정확한 값 계산은 아니다..

softmax에서 표준편차가 클수록 원래 값들 중에서 큰 값에 몰리도록 확률분포가 계산된다. 표준편차가 작을수록 확률분포는 표준편차가 클 때에 비해서 보다 고르게 나타난다.

즉, dimension의 크기가 커질수록 본래 의도하고자 했던 확률분포가 아니라 전혀 다른 확률분포가 나올 가능성이 매우 다분하다는 것이다. softmax의 값들 중 특정 확률분포가 본래 의도보다 너무 크거나 작으면 gradient vanishing이 발생할 위험이 발생한다.

따라서 앞서 밝혔던 수학적 사실을 활용해 분산을 원래대로 복구해주자. 즉, $ax+by$에 $\sqrt{2}$를 나눠서 분산에 2를 나누는 효과를 줌으로써 분산이 1이 되도록 한다.

이러한 이유 때문에 transformer에서는 $d_k$로 scaling을 한다. 왜냐하면 $d_k = d_q$다.

Leave a comment

You may also enjoy