Transformer 실습

SDPA

Scaled Dot-Product Attention. transformer를 배우면서 attention이 1개만 존재했던 그 모델이다.

위 그림처럼 여러 개의 Q, K, V를 생성하는 것이 MHA이고 한 쌍의 Q, K, V만 생성하면 SDPA.

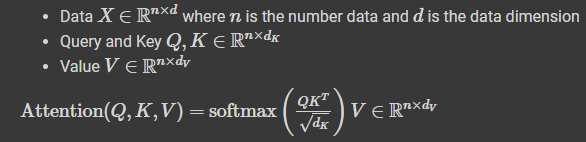
class ScaledDotProductAttention(nn.Module):
    """
    Attention이 1개인 구조.
    입력: embedding 결과인 n차원의 벡터
    
    query, key, value를 찾고 attention 연산을 위의 수식과 같이 수행한다.

    출력: n개의 word vector에 대해서 value vector만큼의 dimension을 가진 tensor
    """
    def forward(self, Q, K, V, mask=None):
        d_K = K.size()[-1] # key dimension
        scores = Q.matmul(K.transpose(-2, -1)) / np.sqrt(d_K)
        if mask is not None:
            scores = scores.masked_fill(mask==0, -1e9)
        attention = F.softmax(scores,dim=-1)
        out = attention.matmul(V)
        return out,attention

# Demo run of scaled dot product attention 

SPDA = ScaledDotProductAttention()
"""
n_batch: n_batch개의 단어가 있음을 의미
d_K: key vector의 dimension
d_V: Value vector의 dimension
n_Q: Query vector의 개수
n_K: Key vector의 개수
n_V: Value vector의 개수
"""
n_batch, d_K, d_V = 3, 128, 256 # d_K(=d_Q) does not necessarily be equal to d_V
n_Q, n_K, n_V = 30,50,50
Q = torch.rand(n_batch,n_Q,d_K)
K = torch.rand(n_batch,n_K,d_K)
V = torch.rand(n_batch,n_V,d_V)
out,attention = SPDA.forward(Q,K,V,mask=None)
def sh(x): return str(x.shape)[11:-1] 
print ("SDPA: Q%s K%s V%s => out%s attention%s"%
       (sh(Q),sh(K),sh(V),sh(out),sh(attention)))

수식에서도 나와있듯이, query와 key의 차원은 \(\mathbb{R}^{n\times d_K}\)이다. 즉, query와 key는 동일 차원이어야만 연산이 가능하다.

value의 차원은 \(\mathbb{R}^{n\times d_V}\)이지만 편의상 query, key와 동일하게 구현한다. 즉, 같아도 무방하다.

Q, K, V의 개수

Encoder, decoder가 존재한다면

코드를 보면 SPDA에 대한 vector를 생성할 때 다음과 같이 생성했다.

n_Q \(\neq\) ( n_K = n_V)

encoder에서 V와 K에 대한 정보를 받고 decoder는 decoder에 들어오는 입력으로 Q를 생성하기 때문에 이렇게 수가 달라도 된다.

encoder, decoder를 상정한 것이기 때문에, 이것이 더 일반적이다.

---

SPDA의 목적이 여기서 나온다! Query vector에 대한 encoding을 하고 싶은데, key와 value vector를 참고해서 만드는 것이다.

즉, SPDA의 출력 vector 또한 Query vector와 개수가 같아야 한다.

Self-attention이라면

n_Q = n_V = n_K

모두 같아야한다.

K.transpose(-2, -1)

pytorch의 tensor에 대해서는 위와 같이 transpose가 가능하더라. 즉, 두 개의 인자로 들어온 차원에 대해서 서로 바꿔준다. 위에서는 마지막에서 첫번째 차원과 마지막에서 두번째 차원을 서로 바꿔주는 것이라고 이해할 수 있다.

torch.nn.Softmax()

dim = -1의 의미를 몰라서 docs를 찾아보니 다음과 같다.

dim (int) – A dimension along which Softmax will be computed (so every slice along dim will sum to 1).

https://stackoverflow.com/questions/49036993/pytorch-softmax-what-dimension-to-use

해당 차원에 대해서 softmax를 계산한다는 것 같다.

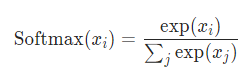
softmax의 정의는 위와 같은데 여기서 \(x_j\)의 j를 dim 옵션을 통해 지정한다.

SDPA를 위해 구현한 코드가 MHA에서도 작동하는 이유

Batch the multiplication이기 때문에 된다고 하셨다. 정확히 뭐라고하신건지는 모르겠다..

내 의견은 어차피 matrix 연산을 통해 SDPA가 구현됐기 때문에 Q, K, V가 몇차원이든 상관없이 연산이 가능하도록 차원의 수만 맞추면 된다는 뜻인 것 같다.

MHA(Multi-head attention)

class MultiHeadedAttention(nn.Module):
    def __init__(self,d_feat=128,n_head=5,actv=F.relu,USE_BIAS=True,dropout_p=0.1,device=None):
        """
        :param d_feat: feature dimension
        :param n_head: number of heads
        :param actv: activation after each linear layer
        :param USE_BIAS: whether to use bias
        :param dropout_p: dropout rate
        :device: which device to use (e.g., cuda:0)
        """
        super(MultiHeadedAttention,self).__init__()
        if (d_feat%n_head) != 0:
            raise ValueError("d_feat(%d) should be divisible by b_head(%d)"%(d_feat,n_head)) 
        self.d_feat = d_feat
        self.n_head = n_head
        self.d_head = self.d_feat // self.n_head
        self.actv = actv
        self.USE_BIAS = USE_BIAS
        self.dropout_p = dropout_p # prob. of zeroed

        self.lin_Q = nn.Linear(self.d_feat,self.d_feat,self.USE_BIAS)
        self.lin_K = nn.Linear(self.d_feat,self.d_feat,self.USE_BIAS)
        self.lin_V = nn.Linear(self.d_feat,self.d_feat,self.USE_BIAS)
        self.lin_O = nn.Linear(self.d_feat,self.d_feat,self.USE_BIAS)

        self.dropout = nn.Dropout(p=self.dropout_p)
    
    def forward(self,Q,K,V,mask=None):
        """
        :param Q: [n_batch, n_Q, d_feat]
        :param K: [n_batch, n_K, d_feat]
        :param V: [n_batch, n_V, d_feat] <= n_K and n_V must be the same 
        :param mask: 
        """
        n_batch = Q.shape[0]
        Q_feat = self.lin_Q(Q) 
        K_feat = self.lin_K(K) 
        V_feat = self.lin_V(V)
        # Q_feat: [n_batch, n_Q, d_feat]
        # K_feat: [n_batch, n_K, d_feat]
        # V_feat: [n_batch, n_V, d_feat]

        # Multi-head split of Q, K, and V (d_feat = n_head*d_head)
        """
        Q, K, V를 분할해준다. 가령 (100,)이라고 하면 (10,10)으로 만들어준다.
        여기서는 d_feat을 n_head개로 분할해 d_head 차원으로 만들었다.
        """
        Q_split = Q_feat.view(n_batch, -1, self.n_head, self.d_head).permute(0, 2, 1, 3)
        K_split = K_feat.view(n_batch, -1, self.n_head, self.d_head).permute(0, 2, 1, 3)
        V_split = V_feat.view(n_batch, -1, self.n_head, self.d_head).permute(0, 2, 1, 3)
        # Q_split: [n_batch, n_head, n_Q, d_head]
        # K_split: [n_batch, n_head, n_K, d_head]
        # V_split: [n_batch, n_head, n_V, d_head]

        # Multi-Headed Attention
        d_K = K.size()[-1] # key dimension
        scores = torch.matmul(Q_split, K_split.permute(0, 1, 3, 2)) / np.sqrt(d_K)
        if mask is not None:
            scores = scores.masked_fill(mask==0,-1e9)
        attention = torch.softmax(scores,dim=-1)
        x_raw = torch.matmul(self.dropout(attention),V_split) # dropout is NOT mentioned in the paper
        # attention: [n_batch, n_head, n_Q, n_K]
        # x_raw: [n_batch, n_head, n_Q, d_head]

        # Reshape x
        x_rsh1 = x_raw.permute(0,2,1,3).contiguous()
        # x_rsh1: [n_batch, n_Q, n_head, d_head]
        """
        n_head개로 d_head차원만큼 분할됐던 tensor를 합쳐준다.
        n_head * d_head = d_feat니까 바로 d_feat를 사용한다.
        """
        x_rsh2 = x_rsh1.view(n_batch,-1,self.d_feat)
        # x_rsh2: [n_batch, n_Q, d_feat]

        # Linear
        x = self.lin_O(x_rsh2)
        # x: [n_batch, n_Q, d_feat]
        out = {'Q_feat':Q_feat,'K_feat':K_feat,'V_feat':V_feat,
               'Q_split':Q_split,'K_split':K_split,'V_split':V_split,
               'scores':scores,'attention':attention,
               'x_raw':x_raw,'x_rsh1':x_rsh1,'x_rsh2':x_rsh2,'x':x}
        return out

# Self-Attention Layer
"""
n_batch: 학습 데이터 중에서 128개씩 batch 뜯어오겠다.
n_src: n_src만큼의 word가 들어간다. = n_src만큼의 sequence를 한꺼번에 처리하겠다.
d_feat: feature의 차원
n_head: multi-head attention을 몇개로 할건지
"""
n_batch = 128
n_src   = 32
d_feat  = 200
n_head  = 5
src = torch.rand(n_batch,n_src,d_feat)
self_attention = MultiHeadedAttention(
    d_feat=d_feat,n_head=n_head,actv=F.relu,USE_BIAS=True,dropout_p=0.1,device=device)

# self attention이니까 모두 같은 차원으로 Q, K, V가 구성된다.
out = self_attention.forward(src,src,src,mask=None)

Q_feat,K_feat,V_feat = out['Q_feat'],out['K_feat'],out['V_feat']
Q_split,K_split,V_split = out['Q_split'],out['K_split'],out['V_split']
scores,attention = out['scores'],out['attention']
x_raw,x_rsh1,x_rsh2,x = out['x_raw'],out['x_rsh1'],out['x_rsh2'],out['x']

\[head_{\color{red}i} = \text{Attention}(Q {\color{green}W}^Q_{\color{red}i},K {\color{green}W}^K_{\color{red}i}, V {\color{green}W}^V_{\color{red}i})\]

• 논문에는 dropout이 없다. 하지만 실제로는 dropout을 모든 attention에서 사용하기 때문에 사용했다.
• 원래의 MHA는 k개의 header를 여러개 만들고 나중에 이 결과들을 aggregate한다.
  • 실제 구현은 미리 k개로 분할하고 Scaled Dot Production을 진행한다.
  • 따라서, d_feat은 n_head로 분할 가능해야 한다.

torch.Tensor.permute

transpose와 동일한 기능이다. 다만, transpose는 두개의 차원에 대해서만 치환이 되고 permute는 모든 차원에 대해서 가능하다.

결론

약간 헷갈릴 수 있는데 정리하면 아래와 같다.

1. n_Q \(\neq\) ( n_K = n_V)
2. d_Q = d_K

1번이 성립하는 이유

• Key와 Value는 encoder에서 넘어오는 정보
• Query는 decoder에 입력으로 받는 정보

2번이 성립하는 이유

• attention을 계산할 때, Query와 Key를 inner product 해야하기 때문
• Value의 차원은 두 vector와 달라도 되고 같아도 무방